강화학습 논문 리뷰 연재 다섯 번째입니다.
TMI이긴 하지만, 요즘 혼자서 블로그에 논문 리뷰를 쓰다 보니 진도가 지지부진해지던 참에, RL_Korea의 옥찬호 님께서 RL 논문 리뷰 스터디원을 모집하는 것을 보고 참여를 하게 되었습니다. 이번 논문은 제가 4월 19일에 실제로 스터디 내에서 발표하게 될 내용을 담고 있습니다. 저뿐만 아니라, 다른 분들의 논문 리뷰 자료들까지 포함되어 있는 깃허브 주소는 다음과 같습니다. => github.com/utilForever/rl-paper-study <=
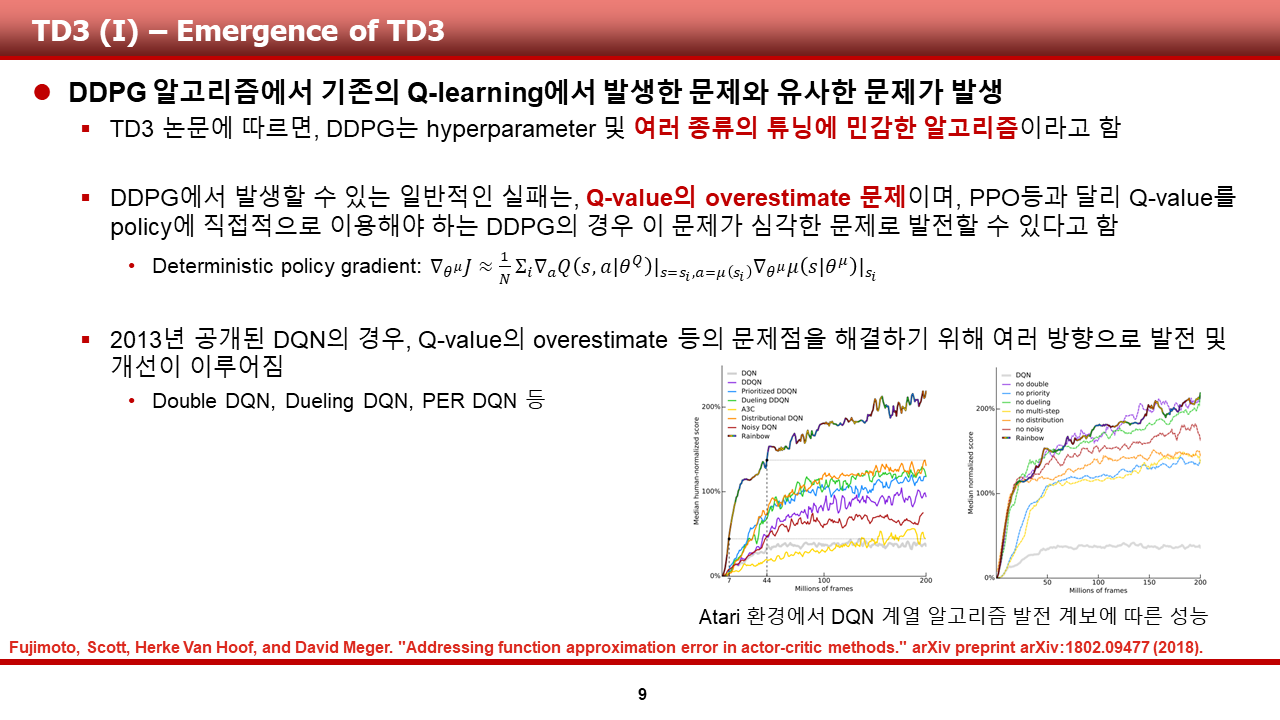
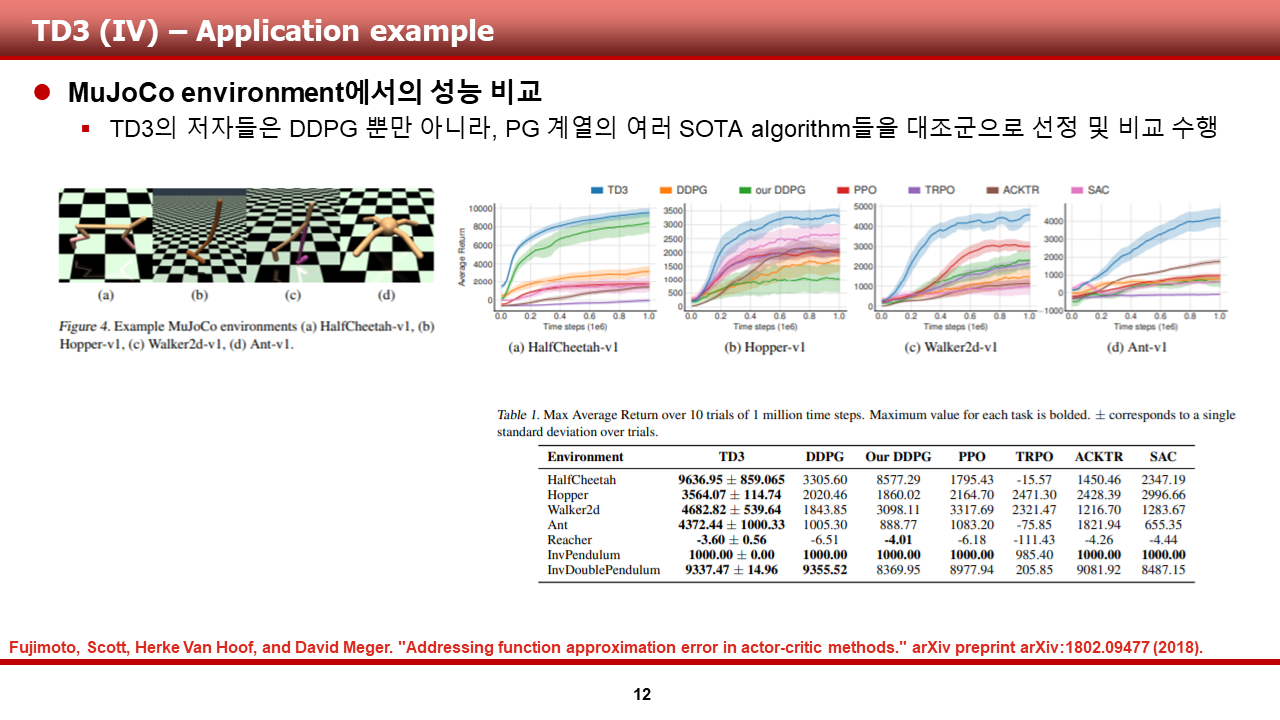
이번 논문 리뷰는, 멀티 에이전트 강화 학습에서 다른 에이전트를 고려하는 것을 시작한 논문인 Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments(이하 MADDPG)에 대한 내용으로 이루어져 있습니다. 이전에 리뷰를 진행했던 TD3와 유사하게, 이 녀석도 DDPG의 친구인 것 같습니다.
그럼, 본격적인 리뷰 시작하겠습니다!

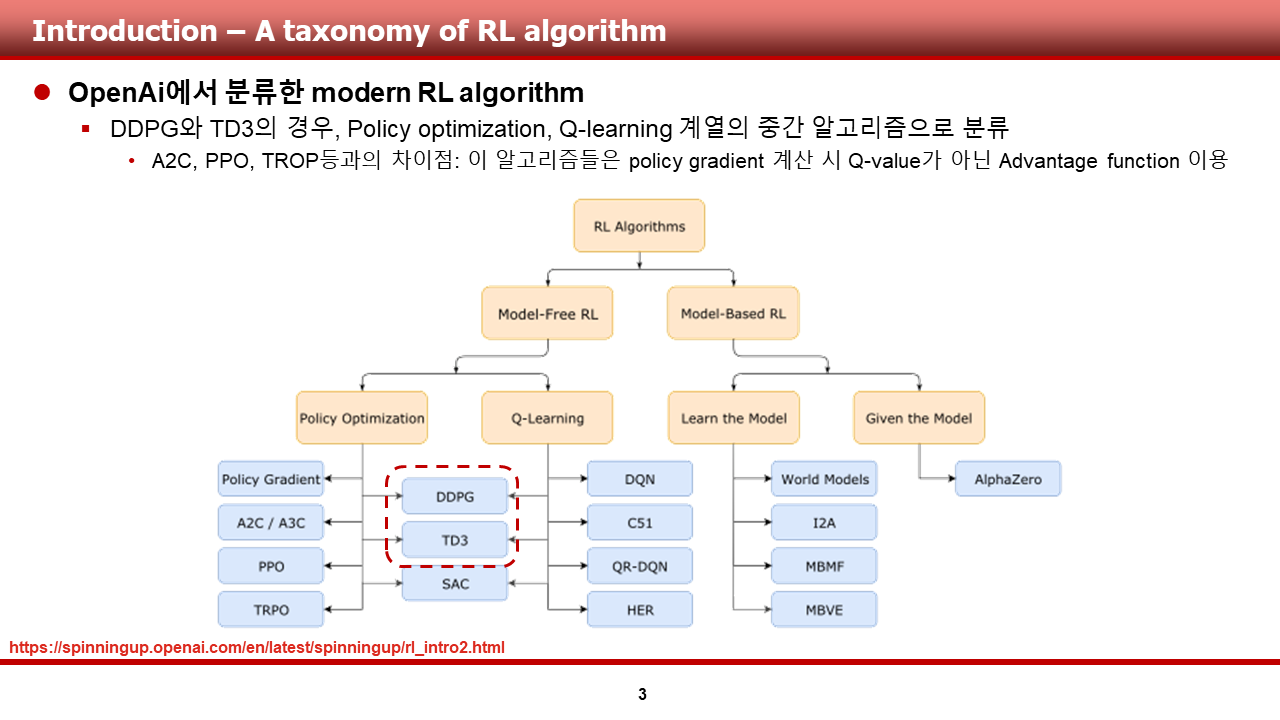
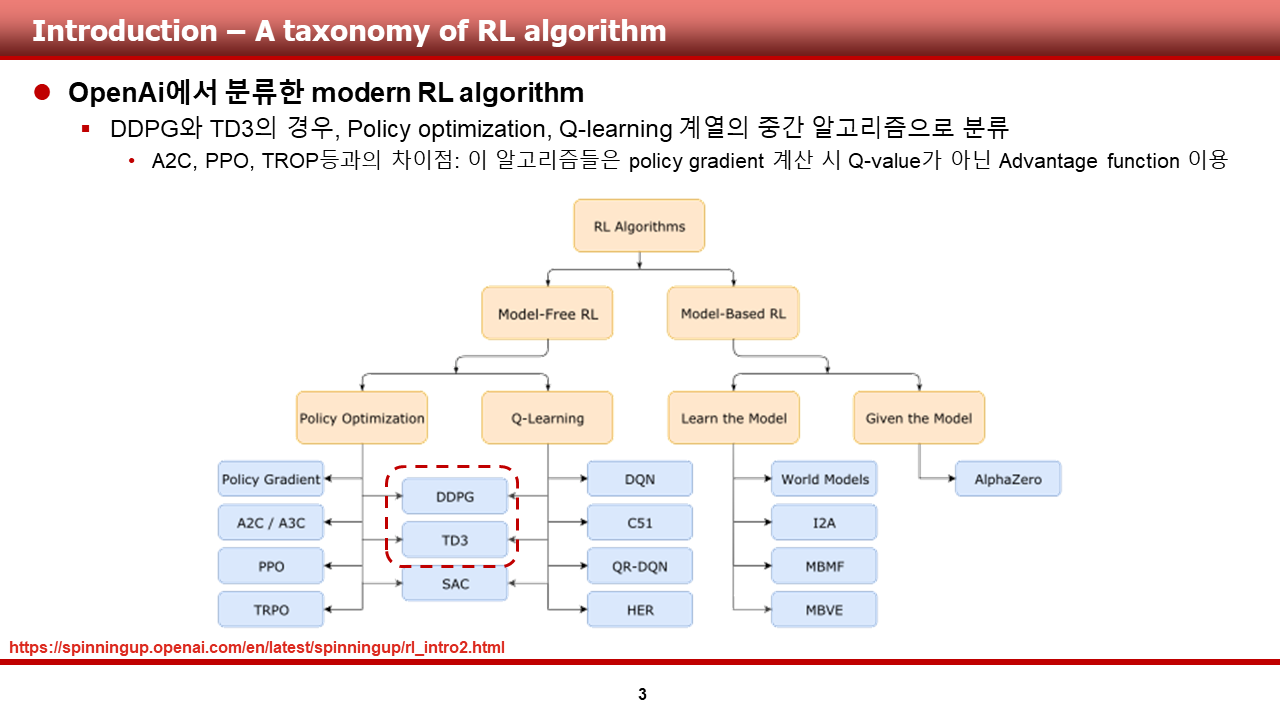
논문의 제목은 상당히 직관적입니다. 협력적이거나, 경쟁적인 행위들이 섞여있는 혼합 환경에서의 Multi-agent actor-critic 알고리즘에 대해 다룰 것만 같은 제목입니다. 실제 논문의 내용도 그러하긴 하지만, 알고리즘이 MADDPG로 불리는 것을 생각했을 때, DDPG 혹은 off-policy 내용이 들어가 있으면 어땠을까 하는 느낌?이 듭니다.

목차는 다음과 같습니다.
가장 먼저, 도입부에서는, 강화학습이 진보해온 과정에 대해서 먼저 간단히 설명을 드린 뒤, MARL에 대한 간단한 소개를, 추가적으로 제가 MADDPG를 적용해본 환경인 pettingZoo environment에 대해서도 소개를 드리도록 하겠습니다.
그 후, 본론에서는, multi-agent domain에서 기존의 기법들이 가지는 한계에 대해서 저자들이 논한 내용에 대해 소개를 드리고, MADDPG를 이해하기 위한 background와, MADDPG에 대한 본 설명을 진행하도록 하겠습니다. 마지막으로, 실험 결과를 같이 한 번 확인해보는 시간을 가지겠습니다!
(이미 MARL에 대한 지식이 있으신 분들과, MARL용 환경이 구성되어 있으신 분들은 도입부를 뛰어넘으셔도 됩니다.)

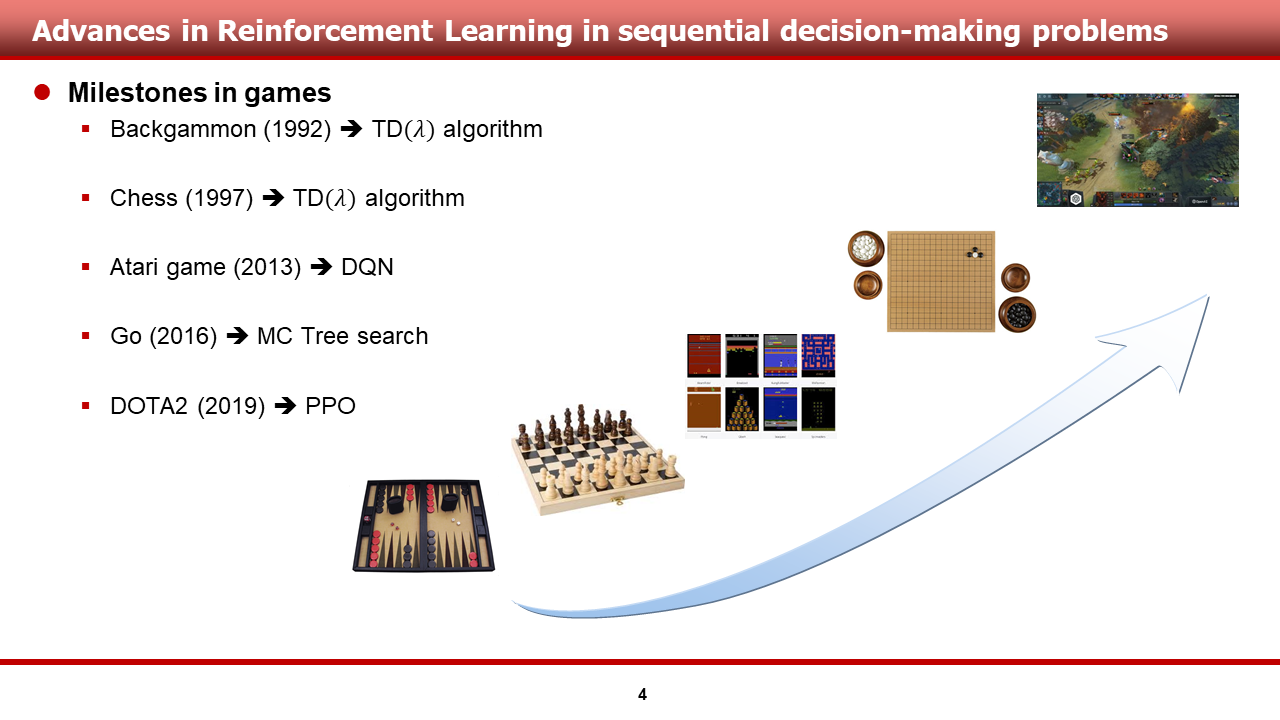
강화학습이 풀고자 하는 문제는 sequential decision-making problem. 즉, 순차적 의사결정 문제입니다. 이러한 순차적 의사결정 문제들에서 강화학습은 굉장한 성과를 보여왔습니다. 슬라이드를 보시게 되면, 강화학습은 1992년 TD lambda 알고리즘을 이용하여 backgammon을 푼 것을 시작으로, 2016년에는 알파고가 바둑(Go) 세계 챔피언인 이세돌을 꺾는 것을 전 세계 시청자들이 보기도 하였습니다. 최근에 얻은 성과 중 괄목할만한 성과로는, 2019년 DOTA2라는 5 vs 5 multi-player game에서 Open AI의 Five가 세계 챔피언을 이기는 성과를 거둔 것이 있습니다. (스타 2도 있습니다!!)
그런데, 바둑에서 DOTA2로 문제가 어려워짐에 있어서, 단순히 게임 내 경우의 수가 증가한 것뿐만 아니라, player 자체가 늘어났다는 것을 눈치채신 분이 계실 겁니다. 맞습니다..! 강화학습의 연구가 알고리즘의 개선뿐만 아니라, single agent에서 multi-agent로 나아가고 있다는 것입니다. 이어지는 장에서 multi-agent 관련 내용을 말씀드리겠습니다.

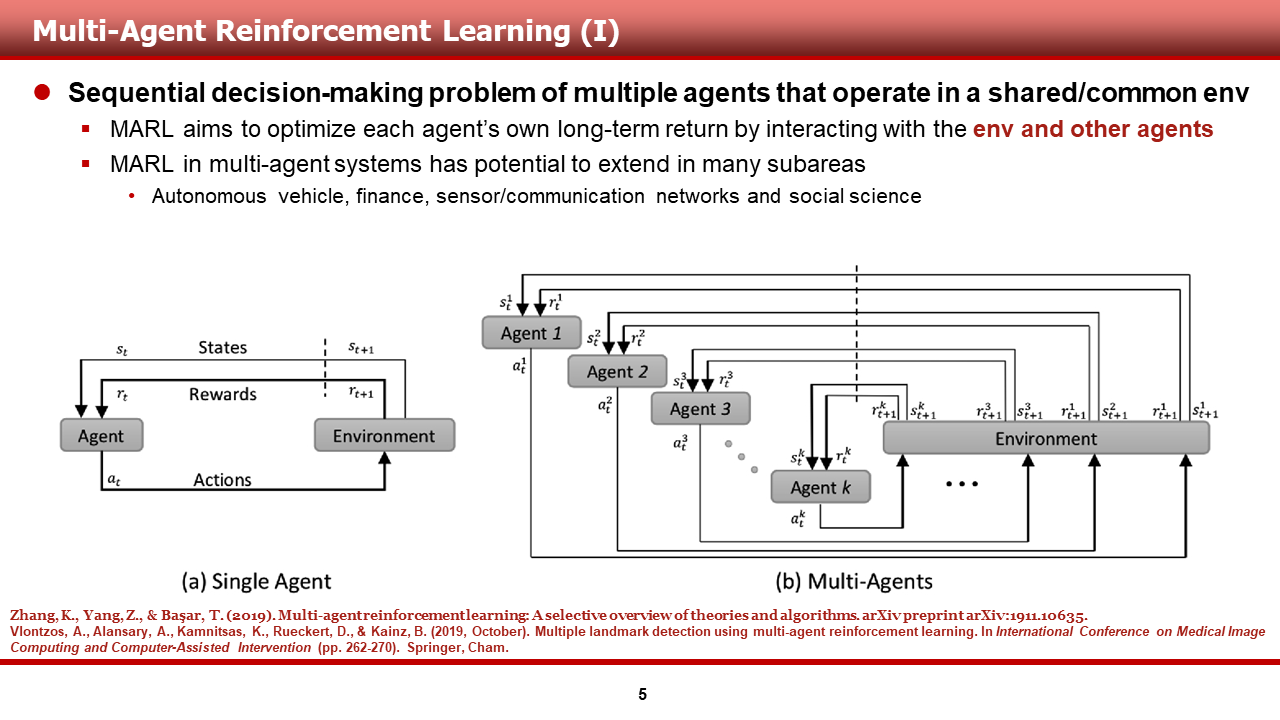
multi-agent RL은 도타와 같은, multi-agent가 동작하는 공통의 혹은 공유하는 환경 내에서 multi-agent들의 순차적 의사 결정 문제를 푸는 것을 목표로 하고 있습니다.
그림 (a)를 보시면, 기존의 강화학습(single-agent RL)의 경우, agent와 environment 사이 상호작용만을 고려하여, agent가 받을 보상을 최대로 하는 것을 목적으로 합니다. 그런데 (b)와 같은 multi-agent setting의 경우, k개의 agent들이 환경과 상호작용하며, 각각의 s a r s'을 주고받는 것을 볼 수 있습니다.
이러한 MARL의 경우, 기존의 SARL과는 여러 면에서 다른 접근을 해서 문제를 해결해야 하며, 이번에 리뷰할 MADDPG 알고리즘이 그것과 관련된 첫 단추를 끼운 논문이라고 생각해주시면 될 것 같습니다.
또한, MARL이 중요한 이유는, 실제 세상에서 해결해야 하는 많은 문제들(자율 주행 자동차, 금융, 기지국의 통신 분배?, 사회 과학 등)이 multi-agent로 구성되어 있기 때문입니다.
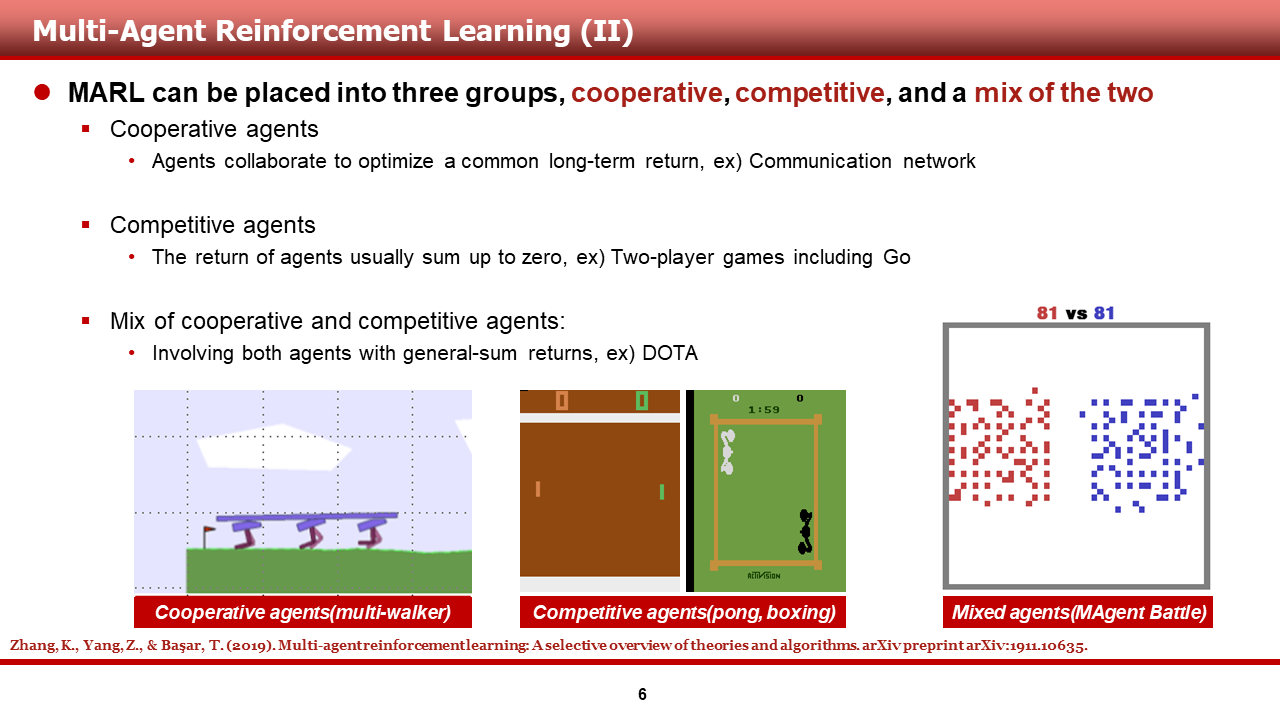
이러한 multi-agent RL은 다음과 같은 세 그룹의 문제를 해결할 수 있어야 합니다.
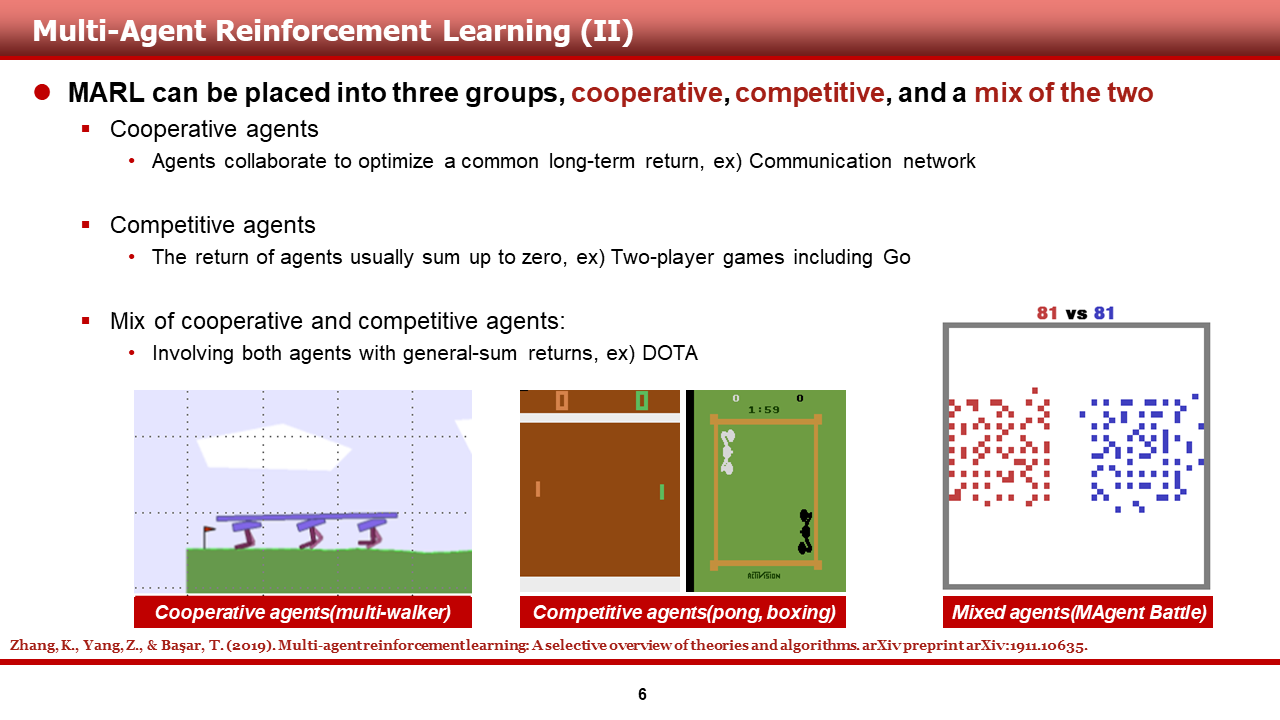
(1) Cooperative setting: 그림의 multi-walker와 같은 협동 게임에서, common long-term return을 최대화하는 문제
(2) Competitive setting: 그림의 multi-player pong, boxing처럼 return의 합이 0인 게임에서, 각기 다른 전략으로 상대를 압도하는 문제
(3) Mix of cooperative and competitive setting: 그림의 군집 전투와 같은 게임에서, 팀 agent끼리는 협동을, 적대적인 agent는 이길 수 있도록 agent를 학습시키는 문제
일반적으로, MARL을 테스트할 수 있는 환경들은 이러한 세 종류의 에이전트를 학습시킬 수 있는 여러 환경들을 포함하고 있습니다. 이번에 참여한 RL 논문 리뷰 스터디가 구현까지가 목적이기 때문에, 저는 어떤 환경에서 MADDPG를 구현해야 할지 조사를 진행하였고, 관련 내용을 다음 슬라이드에서 설명드리겠습니다.

이번 슬라이드에서는 제가 어떤 환경을 테스트 환경으로 골랐는지에 대해서 설명드리겠습니다. 저는 다음과 같은 특징들을 가지는, pettingZoo라고 하는 환경을 선택하였습니다.
먼저, pettingZoo 환경의 경우, 입문자 및 중급자들에게 정말 익숙한, OpenAI의 Gym library와 API가 유사하다는 장점을 가지고 있습니다. pettingZoo 논문의 저자들은, 더 이상 환경마다 다른 세팅에 연구자들이 고통받을 필요가 없다는(이렇게 말하지는 않았습니다.) 문장과 함께, pettingZoo의 API를 설명했습니다.
자세한 사항은, 추후 pettingZoo에 대해 리뷰를 할 때 말씀드리도록 하고, 간단히 언급만 드리면, env.reset(), env.render()등의 친숙한 method들을 포함하고 있으며, env.step()과 유사한 env.last()의 경우, 우리가 알고 있는 (obs, reward, done , info)의 tuple을 출력해 주는 것을 볼 수 있습니다. 저 또한 이 특징 때문에 이 환경을 선택하게 되었습니다.
두 번째 특징으로는, pettingZoo package만 설치하여도, 기존에 연구되던 환경들을 pettingZoo API에 맞게 사용할 수 있도록 저자들이 많은 노력을 들였다는 것입니다. 덕분에 저는 이것저것 여러 환경들을 테스트해 볼 수 있었습니다.

돌고 돌아, 본론인 MADDPG에 대한 설명을 진행하겠습니다.
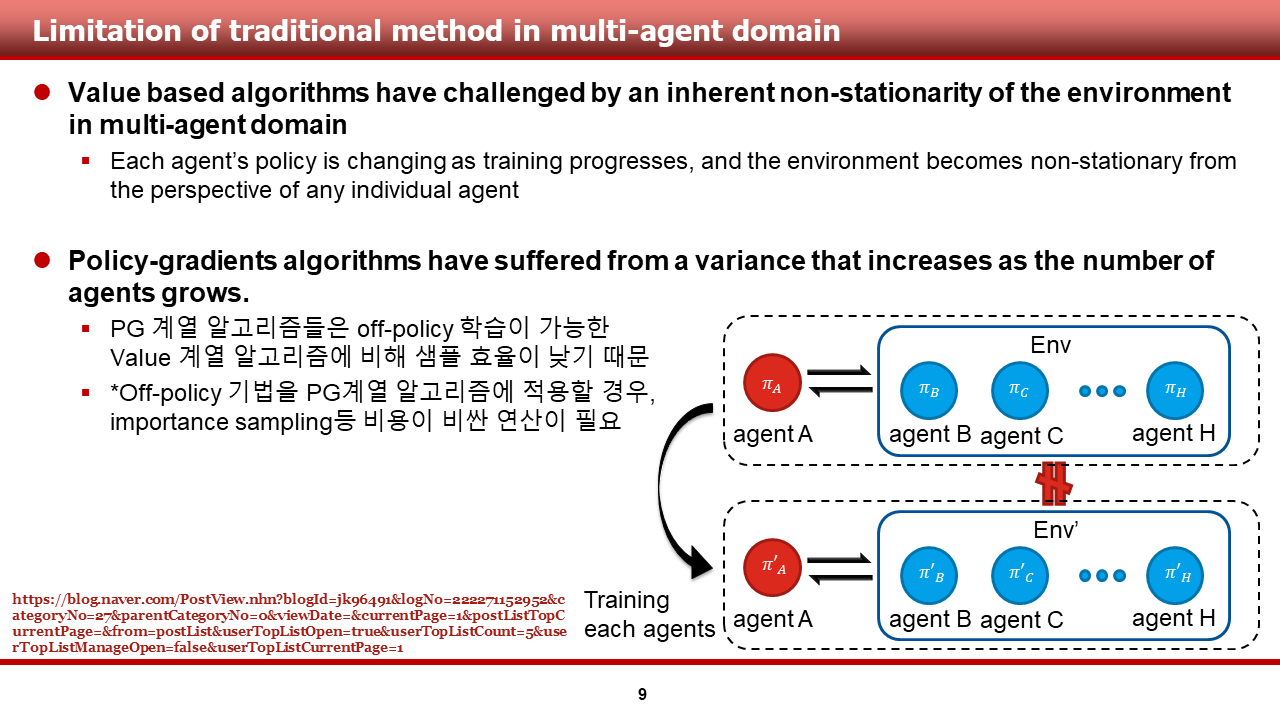
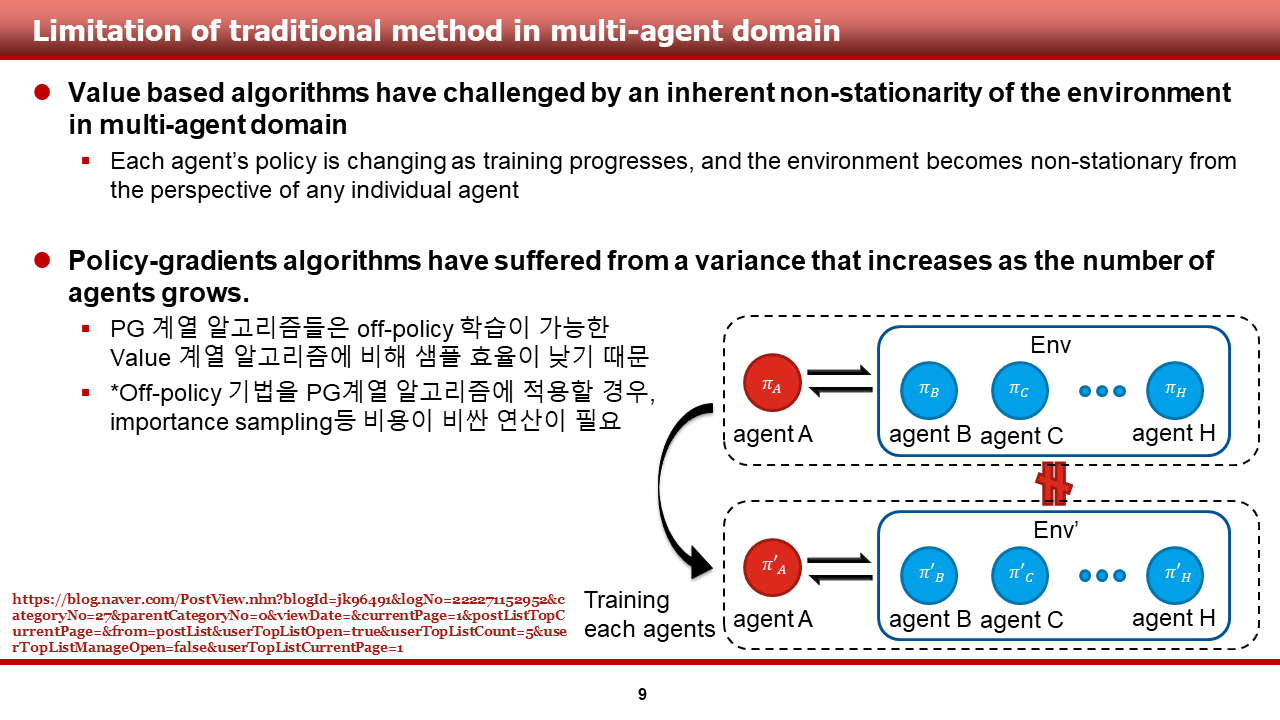
먼저, 논문에 기술되어 있던, multi-agent domain에서의 기존 기법들의 한계점들에 대해 말씀드리도록 하겠습니다. 논문의 저자들은, 기존의 Q-learning 등 value-based algorithm을 multi-agent domain에 적용하는 경우, multi-agent가 존재하는 환경 자체의 non-stationarity로 인해 학습이 어렵다는 것을 지적했습니다.
그 이유는, 오른쪽 그림을 통해 설명드리도록 하겠습니다. multi-agent가 존재하는 환경에서, agentA는 여타 agent인 agentB ~ agentH(웃고 지나가시면 됩니다.)가 존재하는 환경과 상호작용을 하며 sample을 쌓습니다. 그런데, 각 agent가 훈련을 통해 바뀌는 경우, agentA 입장에서는 기존에 sample을 쌓았던 환경이 변하는 것 과 같습니다.(non-stationary) 이전의 연구들은 이를 효과적으로 해결하지 못했다고 지적합니다. (이는 기존의 policy gradient-based algorithm 또한 마찬가지로 겪는 문제인 것 같습니다.)
또한, policy-gradient 기반의 알고리즘의 경우 agent의 숫자가 증가할 경우, high-variance 문제가 발생한다고 서술이 되어 있었습니다. 자세한 내용이 서술되어 있지 않아 구글링을 해 본 결과, 정규열 님의 블로그에서 다음과 같은 사실을 알 수 있었습니다. (blog.naver.com/jk96491/222271152952)
(1) PG 계열 알고리즘은 multi-agent 환경에서 학습 함에 있어서, 일반적으로 off-policy 학습이 가능한 value 계열 알고리즘에 비해 샘플 효율이 낮음
(2) off-policy 기법을 PG 계열 알고리즘에 적용할 경우, importance sampling 등 비싼 연산이 필요

이번 장에서는, 원문에도 있던, 제안된 방법론을 이해하기 위한 배경 지식에 대해 다루고 넘어가도록 하겠습니다.
Multi-agent RL의 경우, MDP를 수학적 framework로 사용하는 SARL과 달리, Markov games를 수학적 framework로써 사용하고 그 안에서 문제를 해결합니다. 이는 간단히 말해 MDP의 multi-agent로의 extension이며, 게임 이론에 그 근간을 두고 있습니다.
Markov Games는 <S, A1, A2, ... AN, O, T, R1, R2, ... , RN>의 tuple로 구성이 되어 있으며, MDP와 유사하면서도 조금 다릅니다.
(1) 전체 agent의 state space S
(2) agent별로 수행 가능한 action space Ai
(3) agent별로 관측 가능한 observation space O
(4) Transition function T
(5) 각 agent 별로 받을 수 있는 reward Ri
또한, 이 논문은 DDPG의 multi-agent extension의 느낌이므로, deterministic policy(확정적 정책)와 deterministic policy gradient 등도 본격적인 방법론 설명 이전에 설명을 하고 있습니다. 확정적 정책의 경우, 확률적(stochastic) 정책과 달리, mu라는 notation으로 표현하며, 상태 변수 값이 정해질 경우 행동 변수의 값이 확정적으로 정해지는 정책을 의미합니다.
또한, log probability가 포함되어 있던 확률적 정책의 정책 기울기 값과 달리, 확정적 정책 기울기는 수학적으로 조금 더 단순하게 표현되고, off-policy learning을 단순 적용함에 있어 수학적으로 문제가 없게 됩니다. MADDPG는 이러한 기존의 DPG, DDPG의 개념을 차용하였습니다.

본격적인 방법론에 대한 설명에 앞서, 저자들이 자신들이 제안한 algorithm에 대해 어떤 평을 했는지에 대해 소개해드리겠습니다.
(1) 제안된 multi-agent algorithm은 학습 시에는 global한 정보를 이용해 학습하며, 실행(action 추론) 시에는 local한 정보만을 이용함
(2) 몇몇 이전 연구와 달리 multi-agent environment의 dynamics를 학습하려는 시도를 수행하지 않음
(3) agent가 global한 정보를 이용해 학습할 시 문제가 되는 '통신'이슈에 대해 특정한 가정을 첨가하지 않음
(4) 제안하는 알고리즘의 경우, 협력적인 행위, 경쟁적인 행위, 혼합 행위 모두 학습이 가능한 알고리즘이며, 저자들 자신이 general multi-agent learning algorithm이라고 평함
다음 슬라이드부터는 이러한 평가를 내린, MADDPG 알고리즘에 대해 본격적으로 다루도록 하겠습니다.

MADDPG가 기존의 RL method와 가장 큰 차이를 가지는 점은 바로, centralized training with decentralized execution(CTDE) 컨셉입니다. 이는, 학습 시에는 다른 agent의 observation을 포함하여 더욱 많은 정보를 통해 학습 하고, action 추론시에는 local information만으로 추론을 하겠다는 컨셉입니다.
이러한 컨셉을 가져가게 될 경우, 각 agent가 상호작용하는 환경의 dynamics인 P가 MDP에서의 P(si' | si, ai)가 아닌, Markov games의 T(s' | s, a1, ... , ai, ..., aN)임을 의미하며, 확정적 정책에 따라, T안에 정책이 포함되어도 문제가 없습니다. 이는, policy changing에 따른 non-stationary 문제가 다소 완화될 수 있음을 의미합니다.
오른쪽 하단의 그림을 보시게 되면, training 시에는 각 agent의 Q_1, ... Q_N이 모든 observation을 사용하여 학습되고, agent i는 Q_i 값을 pi_i 값을 update에 사용하지만, 실제로 action을 추론하는 pi_i는 local information만을 이용하는 구조임을 알 수 있습니다.
이러한 컨셉을 적용할 경우 Critic target, loss와 Deterministic policy gradient는 슬라이드에 도시되어 있습니다.

또한, 저자들은 이전 슬라이드의 핵심 개념과 더불어, MADDPG를 실제 문제에 적용함에 있어 생길 수 있는 여러 문제들에 대한 고민도 추가로 수행하였습니다.
그중 첫 번째 문제는 다음과 같습니다. MADDPG의 경우, centralized Q를 학습하기 위해 사용되는 target Q(y_i)식에서, 다른 agent의 정책을 필요로 하게 되는 문제가 있습니다. 실제 세상에선 이를 항상 알 수는 없기에, 저자들은 다른 agent들의 정책을 approximation하여 target Q 계산 시 사용할 수 있는 방안에 대해서 설명합니다.
그 방법은, agent i가 agent j의 true policy를 parameter phi를 이용해 근사하는 것이며, phi에 따른 approximate policy of agent j의 loss식 또한 슬라이드에 도시된 식으로써 제안하였습니다. loss 식은 일반적인 policy gradient 식으로 되어 있으며, entropy regularizer term이 추가되어 있는 것을 볼 수 있습니다.
저자들은, 이와 같이 추론된 policy를 target Q 계산 시 사용할 수 있으며, target Q 계산 이전, 그러니까 centralized Q function의 업데이트 이전에 approximate policy 업데이트를 수행하는 방법을 통해, 다른 agent의 정책을 모르는 상태에서도 제안한 알고리즘의 활용을 가능케 하였습니다.

두 번째로, 저자들은 경쟁적인 행위를 학습함에 있어, 상대의 현재 전략(정책의 뉘앙스)을 이기기 위해 나의 전략이 매몰되지 않도록(오버 피팅의 뉘앙스), agent별로 K개의 sub-policy를 두어, 이를 ensemble하여 사용할 수 있도록 하는 트릭을 제안하였습니다.
이는 DeepMind의 Alpha star에서 league training을 하는 것과 유사한 컨셉을 조금 더 낮은 레벨에서 구현한 것 같다는 느낌이 들었습니다. (league training은 agent 자체를 여러 개 두어 학습을 수행하는 컨셉)
이러한 두 가지의 추가적인 고민에 대한 실험도 실험 결과에 포함되어 있으며, 다음 슬라이드부터는 실험 결과에 대해 설명 드리도록 하겠습니다.

먼저, 저자들이 실험을 수행한 환경에 대해 간단히 소개해드리고 넘어가도록 하겠습니다. 저자들은 multi-agent particle environment라고 하는 환경에서 실험을 수행하였습니다. 저자들은 이 환경 내의 여러 게임들에 대해 학습을 수행하였는데, 그중 그림이 포함되어 있는 4개의 환경에 대해 간단한 소개가 슬라이드에 기술되어 있습니다.
Physical deception은 해석은 하였으나 지면이 부족하여 생략... 이 장에서는 각 게임이 협동 게임인지, 경쟁 게임인지만 보시고 넘어가면 될 것 같습니다.

이 장에서는, 실험 결과를 설명드리도록 하겠습니다. 저자들은 논문에서 크게 3가지 실험 결과를 제공하고 있습니다. 각각은 다음과 같습니다.
(1) MARL 기법인 MADDPG와 SARL 기법인 TRPO, DDPG 등 기존의 기법들의 비교
하단 가장 왼쪽의 그래프는 cooperative communication(cooperative setting)문제를 학습했을 때의 success rate를 보여줍니다. 기존 SARL 기법은 25000 episode를 학습하는 동안 좋은 결과를 보이지 못하지만, MADDPG의 경우 압도적으로 좋은 결과를 보인다는 것을 알 수 있습니다.
(2) approximate policy 사용 유무에 따른 성능 차이 분석
하단 중앙의 두 번째 그래프(Figure 7 - (a))는 다른 agent의 정책을 완벽히 아는 경우(파란색)와 그렇지 못한 경우(빨간색) MADDPG의 success rate 성능을 보여줍니다. 그래프를 보면 알 수 있듯, approximate policy 사용 시에 성능 하락이 거의 일어나지 않음을 알 수 있습니다.
하단 중앙의 세 번째 그래프(Figure 7 - (b))는 실제 agent의 정책과 approximate policy 사이 차이를 KL-divergence를 이용하여 보여주고 있습니다. 빨간색(listener)과 파란색(speaker)의 차이는 존재하지만, true policy와 approximate policy가 점점 가까워진다는 것을 이 그래프를 통해 보여주고 있습니다.
(3) Policy ensemble 적용 유무에 따른 효과 분석
하단 가장 우측의 그래프는, 경쟁적 행위에서 policy ensemble 사용 시 효과를 비교하는 그래프입니다. agent와 적대적 agent에 대해 ensemble policy 사용 유무에 따라 4가지 case를 실험한 결과, agent가 ensemble policy를 사용하고, adversary가 single policy를 사용할 때 normalized score가 가장 높았음을 지적하며, ensemble policy의 효과를 보여주고 있습니다.
*현재 MADDPG는 구현이 완료 되었으며, 며칠 안으로 대조군인 DDPG 등을 테스트 한 후 결과도 올릴 수 있도록 하겠습니다.
오랜만에 글을 쓰게 되었는데, 길고 긴 이 글 읽어주신 분이 계시다면 정말 감사드립니다.
최근 리뷰했던 논문들 중 난이도가 가장 높았기에, 어려운 점이 있으시면 댓글로 질문 부탁드립니다.
논문의 링크와, 전체 슬라이드는 밑에 준비되어 있습니다.
Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments
We explore deep reinforcement learning methods for multi-agent domains. We begin by analyzing the difficulty of traditional algorithms in the multi-agent case: Q-learning is challenged by an inherent non-stationarity of the environment, while policy gradie
arxiv.org











'Reinforcement Learning > Multi-agent RL' 카테고리의 다른 글
| Paper review of RL (5-2) MADDPG vs TD3 vs DDPG (2) | 2021.06.01 |
|---|---|
| Paper review of RL (1) Dota2 with Large Scale Deep Reinforcement Learning (OpenAI "Five") (0) | 2020.07.11 |