Seungeon

 이 글에서는, 강화학습 논문 리뷰 다섯 번째 연재글에서 리뷰했던 MADDPG의 성능을 확인하기 위해, 기존의 TD3, DDPG와 비교한 결과를 공유하려 합니다.

 구현은 RL_Korea의 옥찬호님이 주도하시는 RL 논문 리뷰 스터디 (4기)에 참여하며 수행하였습니다. 저 뿐만 아니라, 다른 분들의 논문 리뷰 자료들까지 포함되어 있는 깃허브 주소는 다음과 같습니다.  github.com/utilForever/rl-paper-study

그럼 본격적인 리뷰 시작하겠습니다!

 논문의 제목은 다시 보아도 직관적입니다. 협력적이거나, 경쟁적인 행위들이 섞여있는 혼합 환경에서의 Multi-agent actor-critic 알고리즘에 대해 다룰 것만 같은 이 느낌.. 넘어 가겠습니다!

 목차는 다음과 같습니다.

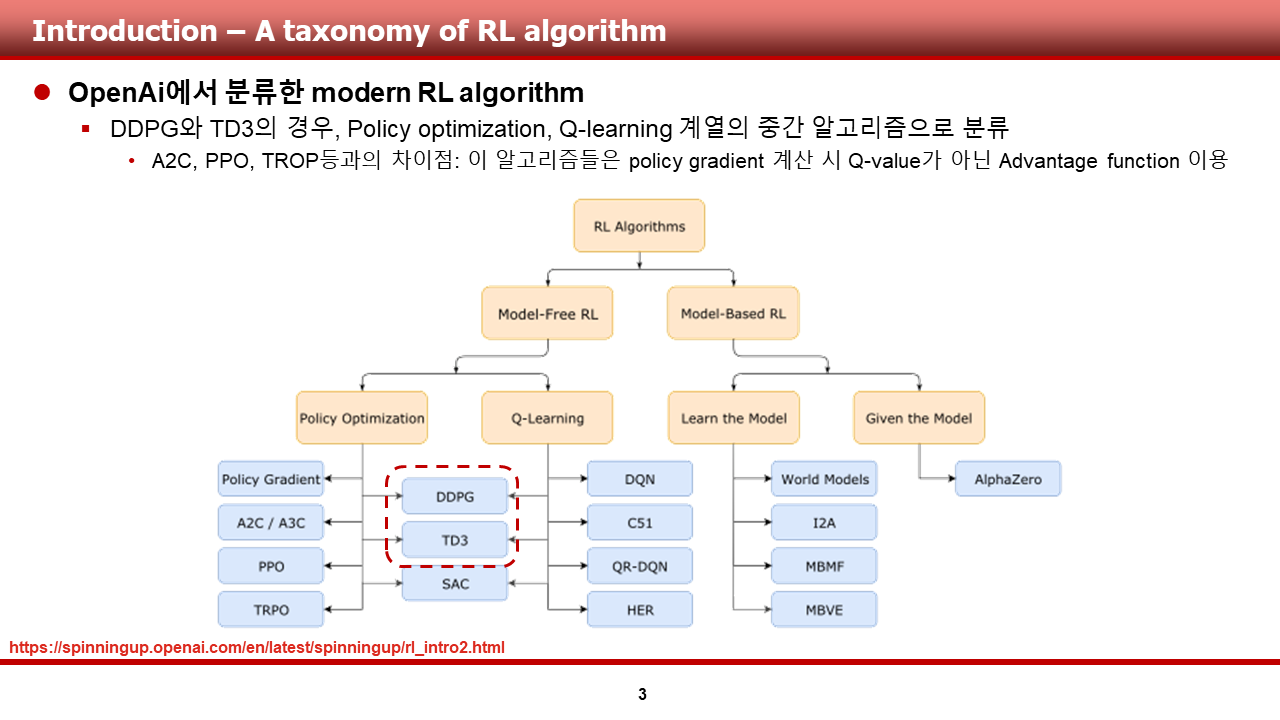
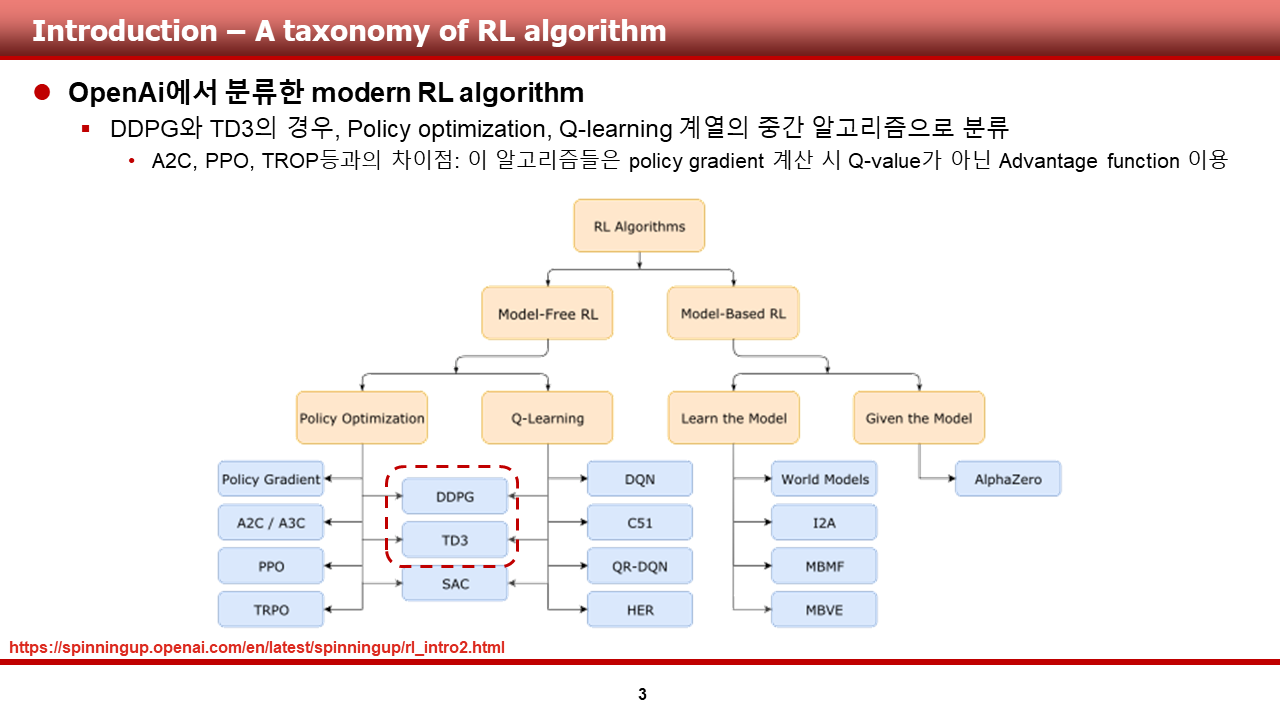
이번 리뷰에서는, 기존의 기법인 DDPG, TD3와 MADDPG 모두 간단한 설명만을 드린 뒤, 적용한 환경에 대한 간단한 소개를, 마지막으로 각 기법들의 시뮬레이션 결과를 공유하고자 합니다.

방법론입니다. 기존의 기법인 DDPG, TD3, 그리고 MADDPG에 대해 한장의 슬라이드로 슥슥 넘어가겠습니다.

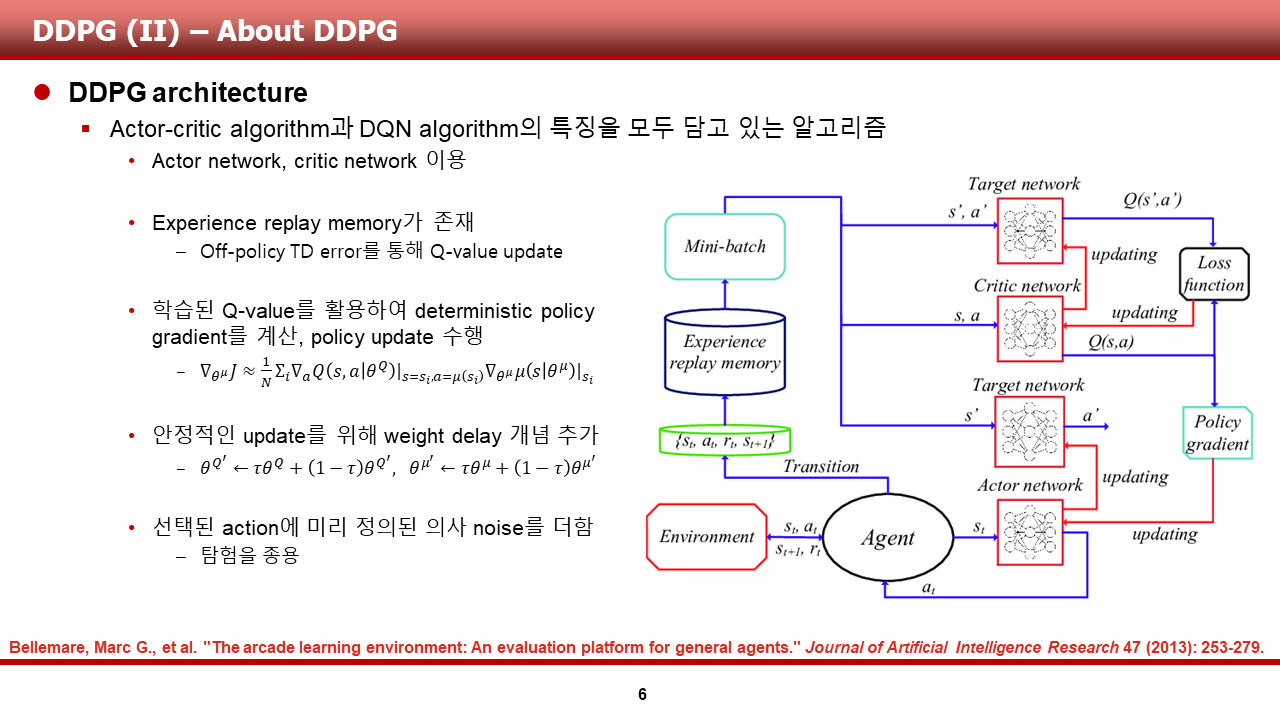
 먼저, DDPG 입니다. DDPG의 경우, 제어 등의 continuous control problem에서 좋은 성능을 보였다고 알려져 있는 알고리즘입니다.

 이 알고리즘의 경우, DQN의 성공 이후 DQN의 여러 특성들을 기존의 DPG 알고리즘에 차용해서 좋은 성능을 보여주었습니다.

  1) Experience replay

     DQN에서 크게 성공을 거둔 이유 중 하나인, 경험 리플레이를 사용

  2) Delayed weight update of target network

     DQN과 같이 n step 고정시키는 방식이 아닌, first order delay를 통해 매 스텝 delayed 업데이트

  3) Deep neural network

     Actor network와 Critic network를 모두 심층 신경망으로 구성

 DDPG의 전신이 되는 DPG 알고리즘의 경우는 다음과 같이 이루어져 있습니다.

  1) Deterministic policy

     특정 상태에 따라, action이 확정적으로 정해지는 정책

  2) Objective function J

     theta로 파라미터화 된 정책의, theta에 따른 목적함수 J를 정의

  3) Deterministic policy gradient

     replay buffer로부터 sample을 꺼내와 업데이트 해도 수학적으로 문제가 없는, policy gradient 식을 정의

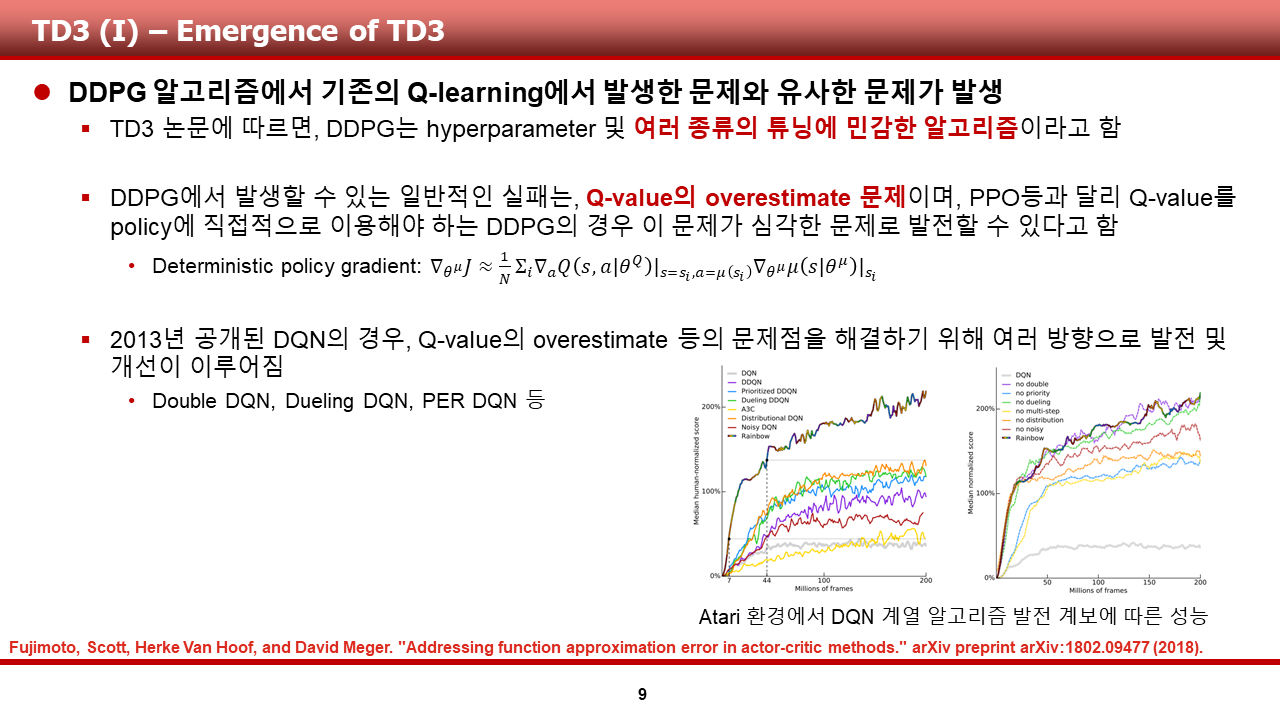
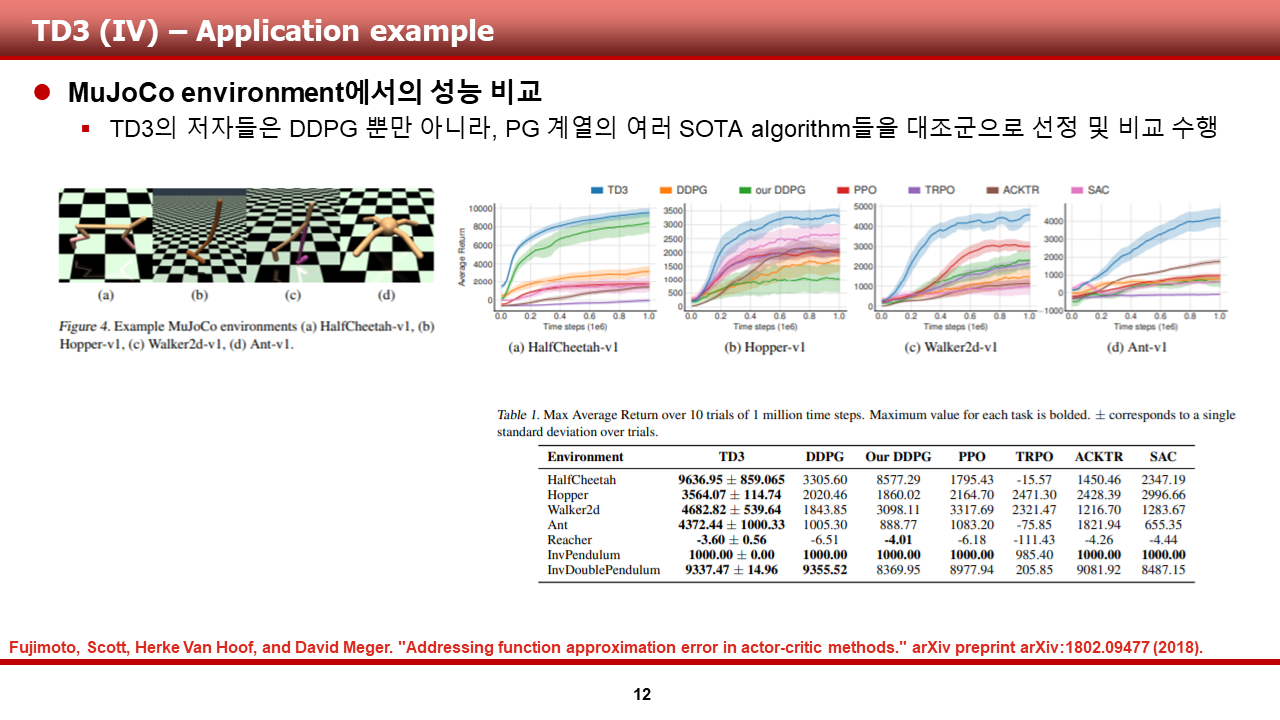
 다음은, TD3 입니다. TD3의 경우, DDPG가 쓰이는 여러 도메인에서 DDPG에 비해 안정적인 수렴 성능을 보여준다고 알려져 있습니다.

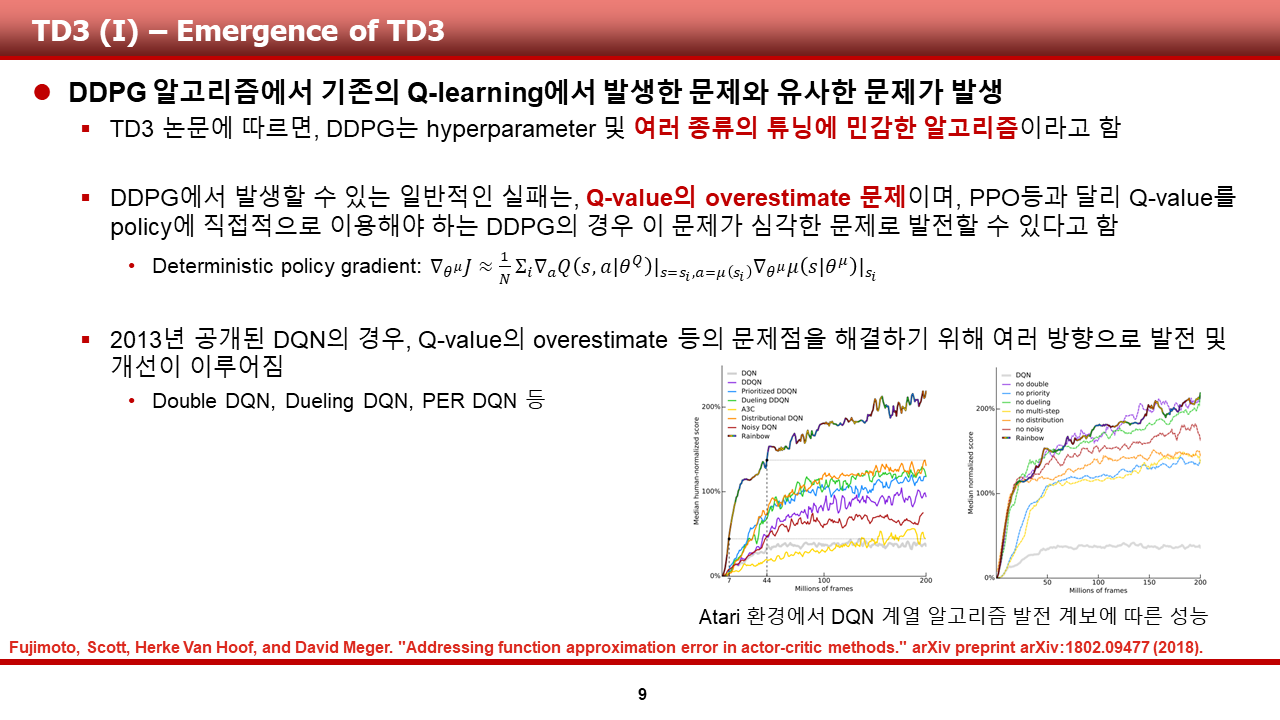
 이 알고리즘의 경우, DDPG에서 발생했던 여러 문제점 중 하나인 Q value의 overestimate 문제를 완화시킬 수 있는 여러 트릭을 사용함으로써 DDPG의 성능을 개선한 알고리즘으로 알려져 있습니다. 그 트릭들은 다음과 같습니다.

  1) Clipped double Q-learning

  2) Delayed policy update

 TD3의 자세한 내용은 제 블로그의 TD3 리뷰 혹은 제가 속해 있는 팀 블로그의 글을 봐주시면 감사할 것 같습니다.

https://seungeonbaek.tistory.com/14

https://ropiens.tistory.com/89

 유사한 이유로, MADDPG도 이번 글에선 생략하고 넘어가도록 하겠습니다.

 시뮬레이션 결과 단락은, 학습이 수행될 환경, 학습 결과의 간단한 분석으로 구성하였습니다.

 먼저, MADDPG를 구현할 환경으로써 저는 SISL환경 내의 multi-walker를 선정하였습니다. 이 환경의 경우, n개의 bipedal walker가 위에 짊어진 꾸러미를 떨어뜨리지 않은 채로 다 같이 전진하는 것을 목적으로 하고 있습니다.

 이 환경의 인수들은 다음과 같습니다.

  1) walker의 대수 (default 3 대)

  2) 위치/자세의 noise 정도 (default 0.5)

  3) episode 내 max_cycle (default 500 step)

  4) rewards

     전진 시 10 점, 넘어질 시 -10 점, 꾸러미를 떨어 뜨릴시 -100점

     (-100 점이라니, 협업을 하지 않을 경우 굉장히 가혹한 페널티가 존재하는 무시무시한 환경입니다..)

 이 환경의 행동 / 관측 정보의 요약은 다음과 같습니다.

  1) Action: 두 다리에 존재하는 두 joint에 가해지는 외력

  2) Observation: 에이전트의 각 축 별 속도, 각, 센서 관측치, 주변 객체들의 상대 위치 .... 등등

 기존의 bipedal walker 문제만 하더라도, 상당히 난이도 있는 continouos control 문제인 것으로 알고 있는데, multi-agent간의 협업을 연구하기 위해 스탠포드가 우물에 독을 푼 것이 아닌가 하는 생각이 들게끔 하는 환경입니다.

 앞서 설명드린 환경에서의 학습 성능은 다음과 같습니다. 총 500 episode 정도 학습을 수행하였으며, 결과만 말씀드리면, MADDPG를 제외하고 두 알고리즘은 학습이 되지 않았습니다.

 그 이유를 저는 다음과 같이 분석하였습니다.

  1) DDPG의 경우: reward 편차가 큰 이러한 환경에서, 개별 agent만을 제어할 수 있는 알고리즘이기 때문에 학습에 어려움을 겪은 것으로 사료됩니다.

  2) TD3의 경우: reward 편차가 크더라도, DDPG보다 안정적인 학습이 가능한 TD3이지만, 개별 agent만을 제어할 수 있다는 한계점으로 인해, 모든 agent가 500 step 동안 가만히 있다가 끝나는 방식으로 학습이 수행 되었습니다.

  3) MADDPG의 경우: 모든 agent의 정보를 받아서 학습을 수행할 수 있으므로, 50 episode 이내로 pacakge를 떨어뜨리지 않는 채로 3 대의 agent가 협력하여 전진하는 것을 확인할 수 있었습니다. (reward > 0)

 사실은 더 많은 step을, 더 많은 agent에 대해 1M, 2M 만큼의 episode를 학습 시켜보면서 결과를 봐야하지만, 노트북이 울부짖는 소리에 마음이 아파 default setting을 해결하는 것 정도에서 학습을 마무리 짓고자 합니다.

 논문 리뷰를 하고 시간이 꽤나 지난 후에 구현 및 결과 분석 글을 쓰니 회사일이 바빴던 건지 제가 게을렀던 건지 아무튼 성찰의 시간을 가져야 할 것 같다는 생각이 듭니다. 오랜만에, 두서 없이 쓴 글이지만, 읽어 주셨다면 정말 감사합니다!!

 논문의 링크와, 전체 슬라이드는 생략하도록 하겠습니다.

강화학습 논문 리뷰 연재 네번째입니다.

이번 논문 리뷰는, 기존의 DeepMind control suite, 상용 동역학 시뮬레이션 프로그램 등의 continuous control 환경에서 좋은 성과를 거둬온 DDPG(Deep Deterministic Policy gradient) 알고리즘을 한단계 진보시킨, TD3(Twin Delayed DDPG)라고 하는 off-policy actor-critic algorithm에 대한 내용을 포함하고 있습니다.

작년과 재작년, 연구실에서 차량의 Adaptive Cruise Control과 관련된 연구를 수행할 때, DDPG를 성공적으로 활용한 논문이 여럿 있는 것을 보고 놀랐던 기억이 있는데, TD3의 경우, 이러한 DDPG에서 발생한 문제를 해결한 알고리즘이라고 하니, 제어 문제에 굉장히 좋은 성능을 낼 수 있는 알고리즘이 아닐까 하는 생각이 듭니다.

그럼, 본격적인 리뷰 시작하겠습니다!

논문의 제목은 직관적이지는 않습니다. "Actor-Critic Methods 에서 발생하는 function approximation error를 다스리기"이지요.

제목이 크게 와닿지는 않지만, 이어지는 내용을 읽으면, 저자들의 의도를 충분히 느낄 수 있는 제목이였던 것 같습니다.

목차는 다음과 같습니다.

가장 먼저, TD3가 포함된, Open AI의 model RL algorithm 분류표를 보며 TD3와 TD3의 전신인 DDPG가 어떤 알고리즘으로 분류되는지 먼저 설명 드리고, DDPG 꼭지에서 핵심 개념인 deterministic policy와 DDPG에 대해 간단히 설명드리겠습니다.

그후, 본론에서는 TD3가 어떠한 이유로 출현하게 되었는지 설명드리기 위해 기존의 DDPG에서 발생한 문제에 대한 설명 드리고, TD3가 어떤 방법으로 이러한 문제를 해결하였는지, 그리고 어떤 환경에 적용하여 TD3의 성능을 검증하였는지에 대해 설명을 드리는 것으로 자료를 준비했습니다.

OpenAI spinningup 사이트를 들어가보면, openAI에서 baseline으로써 제공하는 유명한 알고리즘들 몇몇과 함께, moden RL algorithm을 자체적으로 분류한 사진을 다음과 같이 확인할 수 있습니다.

DDPG와 TD3의 경우, 그림에서 볼 수 있듯이 model-free RL 알고리즘으로 분류할 수 있으며, 세부 계열로는 policy optimization과 Q-learning 계열의 중간 단계로 분류되어 있다는 것을 확인할 수 있습니다.

Policy optimization 계열(PG계열) 알고리즘 중 유명한 A2C/A3C, PPO, TRPO와 DDPG, TD3가 다른 카테고리로 분류가되는 이유는 이 알고리즘들은 policy gradient 계산시 Q-value가 아닌 Advantage function을 활용하고, DDPG와 TD3는 'deterministic policy gradient'계산시 Q-value가 활용되기 때문입니다.

이후의 page에서 DDPG와 TD3에 대한 설명을 이어나가겠습니다.

먼저, DDPG입니다.

DDPG에 대한 본격적인 설명 이전에, deterministic policy와 stochastic policy에 대해 먼저 다루도록 하겠습니다. deterministic policy란, 특정한 state에 대해 action이 확정적으로 정해지는 정책을 뜻합니다. deterministic policy의 경우, 기존에 정책에 사용하던 notation인 pi가 아닌 mu를 notation으로 사용합니다.

Stochastic policy의 경우, 기존에 강화학습 알고리즘들이 다루던 정책이라고 보면 되며, 특정한 state에 대해 action이 확률적으로 정해지는 정책을 뜻합니다. 기존의 PG계열 알고리즘은 이 stochastic policy를 정책으로써 활용하며, 이러한 policy 종류에 따라서, 비단 action을 뽑는 방법 뿐만 아니라 policy gradient 계산식도 달라지는데 이 식은 뒤 슬라이드에서 확인하실 수 있습니다.

이 장에서 추가적으로 알고 넘어가야할 지식은, 상식적으로 생각할 수 있는 사실과는 다르게도 제어, planning등과 같은continuous control problem문제에서 stochastic policy 기반 알고리즘에 비해 deterministic policy 기반의 알고리즘이 성공적인 성과를 이뤄왔다는 것입니다. (주로 DDPG알고리즘과 LSTM등의 RNN 네트워크를 활용하여 많은 성공을 얻어왔습니다.)

그에 대해 논문에서 제공하는 지식과 더불어, 제가 분석한 이유는 다음과 같습니다.

1) continuous control problem의 경우, 필연적으로 high dimensional action space를 가지게 되는데, 이러한 환경에서 stochastic policy에 비해 deterministic policy mu(s)를 활용할 경우, 비교적으로 탐색할 공간이 적어지고, 그에 따라 빠른 수렴이 일어난다는 것입니다.

2) 또한, stochastic policy를 사용하는 PG 계열의 여타 알고리즘과는 달리, off policy 학습이 가능하다는 장점이 있기 때문에, 많은 sample들을 replay memory에 담아서 학습을 할 수 있다는 장점이 있기 때문입니다. 물론, PPO, A3C등의 알고리즘들의 경우, V-trace를 이용한 semi-off policy 학습이 가능하지만, 이에는 컨셉과 수식의 태생적인 한계가 존재합니다. 

3) 기존의 stochastic policy를 사용하는 PG 계열의 여타 알고리즘의 경우 탐험을 종용하는데 있어서 entropy term을 이용하게 되는데, DDPG와 TD3의 경우, 이러한 복잡하고 튜닝이 어려운 방법을 사용할 필요 없이, action에 미리 정의된 의사 noise를 사용할 수 있다는 것에서 큰 장점을 가진다고 생각합니다.

이어서 2장에 걸쳐 DDPG에 대한 간단한 설명을 진행하겠습니다.

DDPG의 경우, Actor-Critic algorithm과 DQN algorithm의 특징을 모두 담고 있는 알고리즘입니다. 그리하여, 슬라이드 하단 주석된 논문에서 참고한 DDPG arcthitecture를 보시게 되면,

1) Actor network와 Critic network를 통해 각각 Q와 action을 예측하는 것을 확인할 수 있으며,

2) DQN 계열에서 사용한 experience replay memory를 사용하는 것을 확인할 수 있습니다.

3) 또한, 학습된 Q-value를 policy gradient 계산시 직접적으로 사용한다는 것을 확인할 수 있습니다.

추가적으로, 그림에 표현은 되어있지 않지만,

4) 안정적인 update를 위해 target network update시 main network의 weight을 정확히 전달해 주는것이 아니라, delay를 주어 update 시켜준다는 것을 알 수 있습니다.

5) 마지막으로, 미리 정의된 의사 noise를 사용합니다.

이장에서는 OpenAI에서 제공하는 DDPG의 pseudo code를 확인할 수 있습니다. 12, 13 line에서 Q-value가 업데이트 되며, 14 line을 통해 deterministic policy gradient를 예측된 Q-value를 이용해 계산한다는 것을 알 수 있습니다.

또한,  target network의 weight update시 미리 정의된 rho값을 이용해 지연을 가한다는 것을 알 수 있습니다.

이어서, 본론인 TD3에 대한 설명을 진행하겠습니다.

TD3는 다음과 같은 DDPG의 문제점으로 인해 출현했습니다.

1) DDPG는 성능을 내기 위해서, hyperparameter 및 여러 종류의 parameter들의 튜닝 과정을 거쳐야하는 민감한 알고리즘이라고 TD3의 저자들은 얘기하고 있습니다.

2) 그 이유는, DDPG에서 deterministic policy gradient (policy loss)계산 시 Q-value가 직접적으로 사용되는데, 이러한 Q-value가 vanilla DQN에서 사용한 main, target Q-network만으로 학습함에 있어서 overestimate와 같은 문제들이 발생했다는 것입니다. 이부분은 Advantage function을 policy loss 계산시 사용하는 여타 PG계열 알고리즘에 비해 자주 발생하는 문제였다고 합니다.

이러한 문제를 해결하기 위해 TD3 알고리즘이 제안되었으며, 이때 DQN에서 이문제를 해결하기 위해 적용한 방식들에서 영감을 얻은 것 같습니다.

이 장부터는 TD3에 대한 설명을 진행하도록 하겠습니다.

밑의 주석의 논문에서 참고한 TD3 arthictecture를 통해 설명을 드리도록 하겠습니다. TD3의 경우, 몇가지 trick을 통해 DDPG에서 치명적인 Q-value overestimate 문제를 잠재웠습니다.

1) 먼저, vanilla Q-learning에 비해 안정적인 학습을 한다는 것이 증명된 Double Q-learning컨셉을 활용하였습니다. DDQN과는 사뭇 다르게 사용되었으며, target network update시 더 작은 값의 Q-value를 학습에 활용하는 방법을 통해 overestimate를 방지하려고 노력하였습니다.

2) 또한, critic과 actor entwork를 번갈아 업데이트 하던 DDPG와 달리, policy update를 critic network update보다 더욱 적은 빈도로 업데이트 하여, 안정된 Q-value를 policy loss 계산시 사용할 수 있도록 하였습니다.

이 두가지 방법을 통해 DDPG에 비해 hyperparameter에 둔감한 알고리즘을 설계하였으며, 제가 test 해본 결과, MDP parameter인 distcount rate gamma와, weight delay parameter인 tau를 제외하면 batch size, neural network의 hyperparameter등을 수정하여도, 정책이 강건하게 수렴한다는 것을 확인할 수 있었습니다.

OpenAI에서 제공하는 TD3의 psudo code에서는 이러한 과정들이 어떻게 적용되었는지 확인할 수 있습니다. 이 pseudo code에서 아쉬운점은 더 작은 Q-value를 policy gradient 계산시 사용한다는 것이 명시적으로 드러나지 않았다는 것이지만, 그래도 보기좋게, 깔끔하게 서술이 되어 있어 사용하게 되었습니다.

이 장에서는, TD3의 저자들이 TD3를 MuJoCo physice engine에서 다른 PG 계열 SOTA 알고리즘과 비교한 그래프 및 표를 보여드리겠습니다. 저자들은 여러 scenario를 학습 시켰으며, 그중 HalfCheetah, Hopper, Walker, Ant의 그래프를 ppt에 도시해 두었습니다.

결과를 비교해보면,

1) TD3가 다른 PG계열 알고리즘에 비해 월등한 수렴성능을 보여준다는 것과,

2) 수렴한 average return의 값이 다른 알고리즘들에 비해 굉장히 높다는 것을 알 수 있습니다.

물론, ppt에 도시하지 않은 reacher, inverted pendulum, inverted double pendulum의 경우에도 미미하지만 더 높은 성능을 보여준다는 것을 밑에 도시한 표와, 원문에서 확인하실 수 있습니다.

이번에도 긴 글을 읽어주신 점 감사드립니다.

논문의 링크와, 전체 슬라이드는 밑에 준비되어 있습니다.

https://arxiv.org/pdf/1802.09477.pdf

이전다음

0123456789101112