[CS 330 - Lec 4] optional reading paper 단순 정리 (Meta-Learning with Differentiable Convex Optimization)

가짜연구소 5기 멀티태스크메타러닝-초읽기 아카데믹 러너 활동을 통해 위의 논문을 읽게 되었습니다.

제가 주로 다루는 분야가 아니기에, 가볍게 정리하는 느낌으로 가져가 볼까 합니다.

 

Title: Meta-Learning with Differentiable Convex Optimization

Abstract

•  few-shot learning을 위한 많은 meta-learning 접근법들은 nearst-neighbor classifier와 같은 simple base learner들에 의존하고 있다고 합니다.
•  그러나, 심지어 few-shot regime에서도, discriminative하게 훈련된 linear predictor들이 더욱 좋은 일반화 성능을 보여주고 있다고 합니다.
•  저자들은 이러한 predictor들을 few-shot learning을 위한 표현을 학습할 수 있는 base learner로써 사용하고, 그것들이 few-shot recognition benchmark들에서 feature size나 성능 사이의 tradeoff면에서 더욱 이점을 제공할 수 있다는 것을 보여주었다고 합니다.
•  저자들의 목적은 새로운 category들을 위한 linear classification 규칙 아래에서, 일반화가 더욱 잘된 feature embedding을 학습하는 것이라고 합니다. 음?
•  이러한 목적을 효율적으로 달성하기 위해, 저자들은 linear classifier의 두 개의 속성을 십분 활용했다고 합니다: convex problem의 optiality condition의 implicit differentiation 그리고 optimization problem의 dual formulation.
  •  이는 저자들에게 computational overhaed면에서 약간의 증가와 함께, 개선된 high-dimensional embedding의 일반화 성능을 선물로 주었다고 합니다.
• MetaOptNet으로 명명한 저자들의 접근법은 miniImageNet, tieredImageNet, CIFAR-FS 그리고 FC100과 같은 few-shot laerning benchmark들에서 SOTA를 갱신했다고 하며, 코드는 online으로 공개했다고 합니다.

 

Introduction

 몇몇 예제들로부터 학습을 할 수 있는 능력은 human intelligence만이 가진 특징이라고 하며, 이는 modern ML system이 풀어야 하는 숙제로써 남겨져 있다고 합니다.

•  이 문제는 최근 few-shot learning이 meta-learning problem으로 등장하면서, ML community로부터 상당한 관심을 받아왔다고 합니다.

 

 그 녀석들의 목표는 few training example들을 가지는 task들의 분포들 사이에서 일반화 error를 최소화 하는 것이라고 합니다.

•  전형적으로, 이러한 접근법들은 input domain을 특징 공간으로 mapping해주는 embedding model과, 특징 공간을 task variable로 mapping해주는 base learner로 이루어져 있다고 합니다.

 

 Meta laerning objective는 base learner가 task들 사이에서 일반화 성능을 가질수 있도록? embedding model을 학습하는 것이라고 합니다.

•  많은 선택할 수 있는 base learner들이 존재한다고 합니다. 가장 인기 있는 최근접 이웃 기반 분류기와 그들의 variants들은 간단하고, low-data regime에서 잘 동작하는 접근법이라고 합니다.

 

 하지만, discriminative하게 훈련된 linear classifier는 더 좋은 분류 경계를 학습하기 위해, 더 풍부한 negative example들을 활용할 수 있기 때문에, low-data regime안에서, 종종 최근접 이웃 분류기들을 뛰어넘는 성능을 보여준다고 합니다.

•  더욱이, 그 친구들은 model의 capacity가 L1, L2 norm과 같은 적절한 정규화 방법을 이용해 제어될 수 있기 때문에, high dimensional feature embedding을 더 효율적으로 사용할 수 있다고 합니다.

 

 그러므로, 해당 논문에서 저자들은 few-shot learning을 위한 meta-learning based approach를 위해, base learner로써 linear classifier를 사용하는 방안에 대해서 연구를 수행했다고 합니다.

•  해당 접근법은 Figure 1에 도시되어 있으며, linear support vector machine(이하 SVM)이 주어진 labeled training example set을 분류하기 위해, 그리고 동일한 task로부터 새로운 example set들로부터 generalization error를 계산하기 위해 사용되었다고 합니다.

 

 Key challenge는 계산 이슈라고 하며, 왜냐하면 task들 사이의 generalization error를 최소화 하는 meta-learning의 objective는 inner loop of optimization에서의 liniear classifier의 훈련을 필요로 하기 때문이라고 합니다. (그니까 for 문 두 개 돌아서 그렇다는 것 같군요 호호)

•  그러나, linear model의 objective는 convex하고 그래서 효율적으로 해결이 될 수 있다고 합니다.

 

 저자들은 meta-learning을 효율적으로 해줄 수 있는 convex nature로부터 다음의 추가적인 두 가지 속성을 관찰했다고 합니다. (1) Implicit differentiation of the oiptimization, (2) the low-rank nature of the classifier in the few-shot setting.

•  첫 번째 속성은 optima를 추정하기 위해 그리고 embedding model을 훈련하기 위한 KKT conditions 혹은 optimality를 암묵적으로 미분하기 위해 자주 사용되는 convex optimizer들의 사용을 허용한다는 것입니다.
•   두 번째 속성은 dual formation의 최적화 변수들의 숫자가 few-shot learning을 위한 feature dimension에 비해 굉장히 작다는 것을 의미한다고 합니다. 완전 최적화 수학 논문이겠는데요?!

 

 이를 위해, 저자들은 few-shot classification task들을 위한 다양한 linear classifieres(SVMs, linear regression)과 embedding model을 end-to-end learning이 가능하도록, differentiable quadratic programming(이하 QP) solver를 통합했다고 합니다.

•  이러한 속성들을 사용함에 따라, 저자들은 자신들의 기법이 실용적이며, computational cost의 약간의 증가로, 최근접 이웃 classifier에 비해 상당한 이점을 제공할 수 있다는 것을 보여준다고 합니다.

 

 저자들의 기법은 자주 이용되는 benchmark인 miniImageNet, tieredImageNet, CIFAR-FS 그리고 FC100 등에서 5-way 1-shot, 그리고 5-shot classification에서 SOTA 성능을 갱신했다고 합니다.

 

Related work

 Meta-laerning은 learner의 어떤 측면들이 task들의 분포 사이에서 일반화를 효과적으로 할 수 있을지에 대해 연구한다고 합니다.

 

 Few-shot learning을 위한 meta-learning 접근법들은 넓게 3가지 그룹으로 분류하는 것이 가능하다고 합니다.

(1) Gradient-based metdhos

(2) Nearst-neighbor methods

(3) Model-based methods

 

 Gradient-based methods는 training example들에 embedding model parameter를 적응하게 하기 위해, gradient descent를 사용하는 기법들이라고 합니다.

 

 Nearst-neighbor methods는 embedding들에 대해 distance-based prediction rule을 학습하는 것이라고 합니다.

•  예를 들어, prototypical network는 각 class를 example들의 mean embedding으로 표현한다고 하며, 분류 기준은 nearset class mean까지의 거리를 기반으로 한다고 합니다.
•  다른 예제는 matching network라고 합니다. 이 친구는 training data에 대한 embedding을 사용해서 class density들의 KDE를 학습한다고 합니다.

 

 Model- based methods는 model parameter들을 추정하기 위해 parameterized predictor를 학습한다고 합니다.

•  예를 들면, parameter space에서 few steps of gradient descent방법과 유사한 parameter를 예측하는 reccurent network 음…??

 Gradient-based 기법들은 일반적이지만, 그 친구들은 embedding dimension이 성장함에 따라 overfitting하는 경향이 있다고 합니다.

 

 최근접 이웃 접근법들은 단순하며 few-shot setting에 잘 확장 된다고 합니다.

•  하지만, 최근접 이웃 기법들은 feature selection을 위한 메커니즘이 없으며, 또한 noisy feature에 강건하지 않다고 합니다.

 

 저자들의 작업물은 최적화 절차에서의 backpropagation과 연관이 있는 기술이라고 합니다.

•  Domke는 fixed num of steps에 대한 gardient decsent unrolling과 기울기를 계산하기 위한 automatic differentiation기반의 generic method를 제안했다고 합니다.

 

 그러나, trace of the optimizer는 large problem에 대해 금지될 수 있는 기울기를 계산하기 위해 저장할 필요가 있다고 합니다….??

•  storage overhead issue는 Maclaurin 등에 의해 조금 더 자세히 다뤄졌다고 하네용ㅎ 그들은 deep network의 optimization trace의 낮은 표현 정확도를 연구했다고 합니다.

 

 Unconstrained quadratic minimization problem에서와 같이 최적회 문제의 argmin을 해석적으로 찾을 수 있다면, 기울기를 해석적으로 계산하는 것도 가능하다고 합니다.

•  이는 low-level vision problem을 학습하기 위해서 적용되어 오기도 했다고 합니다.
•  관련 연구[3]은 이러한 아이디어로, ridge regression 기반의 learner와 함께 closed-from solution을 사용해서 few-shot model을 학습시키기도 했다고 합니다.
•  저자들은 또한 논문의 독자들에게 Gould et al의 differentiating argmin and argmax problem을 위한 기법을 survey한 논문을 추천해주기도 했네요.

 

 저자들의 접근법은 convex learning problem으로 형식화 될 수 있는 lineaer classifier의 사용을 주장한다고 합니다.

•  특히, objective는 gradient-based technique을 사용하여 global optima를 얻기 위해 효율적으로 풀 수 있는 QP로 형식화 했다고 하네요.
•  더욱이, convex problem의 solution은 implicif function theorem을 이용하는 learner의 역전파를 사용할 수 있게 해주는, convex problem의 KKT condition으로 특정 지을 수 있다고 합니다.

 

 구체적으로, 저자들은 QP와 QP의 gradient를 계산하기 위해 효율적인 GPU routine을 제공하는, Amos와 Kolter의 formulation을 사용했다고 합니다.

•  그것들은 constraint satistaction problem에 대한 표현을 학습하기 위해 해당 framework를 적용했지만, 일반적으로 발생하는 문제의 크기가 작기 때문에, few-shot learning에도 또한 적합하다고 하네요

 

 저자들의 실험은 hinge loss와 l2 정규화를 포함하는 선형 분류기에 초점을 맞추고 있지만, 저자들의 framework는 다른 loss function들 그리고 non-linear kernel들에도 사용될 수 있다고 합니다.

•  예를 들어, [3]에서 이용된 ridge regression learner의 경우에도 저자들의 framework 내에서 구현이 가능하다고 합니다.

 

Meta-learning with Convex Base Learners

 저자들은 먼저, 이전 연구들을 따라 few-shot learning의 meta-learning framework를 유도하고, 그 다음 linear SVM과 같은 convex base learner가 어떻게 이와 통합될 수 있을지에 대해서 다룬다고 합니다.

 

Problem formulation

 Base learner A의 목표는, training set D^train = {(x_t, y_t)}(t=1~T)이 주어지면 predictor y=f(x; \theta)가 unseen test set D^teset ={(x_t, y_t)}(t=1~Q)에 대해 일반화가 잘 될 수 있도록, predictor의 parameter \theta들을 추정하는 것이라고 합니다.

•  training and teset set은 same distribution으로 부터 샘플링 되고, domain은 \phi로 parameterized된 embedding model f_\phi를 사용해서 feature space로 사상된다고, 종종 가정이 된다고 합니다.
•  최적화 기반 learner들에서, parameter들은 training data에 대한 empirical loss와 simpler model을 촉진하기 위한 regularaiation error를 최소화 하기 위해 얻어진다고 합니다. 이는 다음과 같이 쓸 수 있다고 합니다.

 

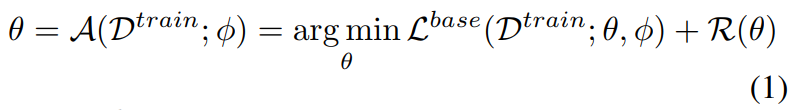
 이때, L^base는 loss function이며, label들에 대한 negative log-likelihood 같은 친구라고 합니다. 그리고, R(\theta)는 regularization term이라고 합니다. 이 정규화 항은 training data가 제한적일때 중요한 역할을 해준다고 합니다.

 

 Few-shot learning을 위한 meta-learning 접근법은 task distribution으로부터 샘플링된 task들의 분포들 사이에서 일반화 오류를 최소화 하는 것을 목적으로 한다고 합니다.

•  구체적으로, 이는 collection of task T={(D^train_i, D^test_i)}_(i=1~I)에서의 learning으로써 생각할 수 있다고 하며, 이는 종종 meta-training set으로 불리운다고 합니다.
•  Tuple (D^train_i, D^test_i)는 training and, test dataset or task를 의미한다고 합니다.

 Objective 는 base learner A가 주어졌을 때, task들 사이에서 generalization error을 최소화 하는 embedding model의 \phi를 학습하는 것이라고합니다.

• 형식적으로, learning objective는 다음과 같아진다고 합니다.

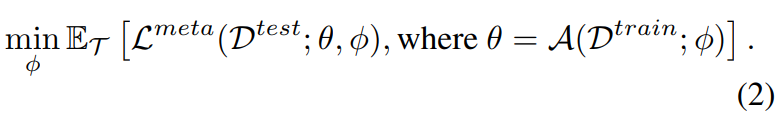
 Figure 1은 single task에 대한 training과 testing을 보여주고 있다고 합니다. 일단 embedding model f_\phi가 학습되면, 그 친구의 일반화는 held-out tasks(종종 meta-test set으로 불리기도 하는) S={(D^train_j, D^test_j)}_(j=1~J)의 집합을 통해서 추정이 된다고 합니다.

 

 이전 연구에 따라, 저자들은 방정식 2와 3의 기댓값을 추정하는 단계를 각각 meta-training and meta-testing으로써 본다고 합니다.

•  Meta-training하는 동안, 저자들은 추가적인 held-out meta-validation set을 meta-learner의 hyperparameter와 best embedding model을 선택하기 위해 사용한다고 합니다.

 

Episodic samplings of tasks

 miniImageNet과 같은 표준적인 few-shot learning benchmark들은 model들을 K-way, N-shot classification task들에서 평가함. 여기서 K는 num of classes이고, N은 num of training examples per class라고 합니당.

 

 Few-shot learning technique은 N이라고 하는 작은 값에 대해서 평가가 된다고 하며, N은 보통 {1, 5}사이에 속하는 값이라고 합니다. 5 shot까지가 보통인가보네용!

•  실제적으로, 이러한 데이터셋들은 명시적으로 tuple (D^train_i, D^test_i_를 포함하지 않는다고 하며, 각 meta-learning을 위한 task들은 meta-training stage동안 일반적으로 episode로 칭하는 단계에서, “on the fly”로 구축된다고 합니다. 으음?

 

 예를 들어, 이전 연구 [32, 33]에서, task (or episode) T_i = (D^train_i, D^test_i)는 다음과 같이 샘플링된다고 합니다.

•  Overall set of categories is C^train. 각 에피소드에서, C^train으로부터 온 K category를 포함하는 categories C_i는 먼저 sampling 됩니다. 그 다음, category별로 N개의 image로 구성된 training (support) set D^train_i = {(x_n, y_n) | n=1, … , N * K, y_n \in C_i}가 sampling 된다고 합니다.
•  마지막으로, category별로 Q개의 image로 구성된 the test(query) set D^test_i = {(x_n, y_n) | n=1, … , Q * K, y_n \in C_i}가 sampling 된다고 합니다.

 

 저자들은 일반화 에러를 최적화 하기 위해, 해당 과정에서 replacement 없이 sampling했다는 것을 강조하고 있습니다. 다시 말해서, D^train_i와 D^test_i의 교집합이 공집합이라는 것을요!

•  같은 방식으로, meta-validation set과 meta-test set도 C^val 그리고 C^test로부터 on the fly로 구축이 된다고 합니다.

 

 Embedding model의 unseen categories에 대한 일반화 능력을 측정하기 위해, C^train, C^val 그리고 C^test는 상호 분리적으로 선택이 되었다고 합니다.

 

Convex base learneres

 base learner A의 선택은 Equation 2에 대해 상당한 임팩트를 가지고 있다고 합니다.

•  \theta = A(D^train ; \phi)를 계산하는 base learner는 효율성을 가지고 있어야 하는데, 왜냐하면 expectation이 task들의 분포로부터 계산이 되기 때문이라고 합니다.

 

 게다가, embedding model의 \phi를 추정하기 위해, task test error L^meta(D^test; \theta, \phi)의 \phi에 대한 gradient들이 효율적으로 계산이 되어야 한다고 합니다.

•  이는 base learner의 매개변수가 계산하기 쉽고 objectiver가 미분 가능한, nearst class mean과 같은 base learner를 사용하는 이유가 되어 왔다고 합니다.

 

 저자들은 objective가 convex한 multi-class linear classifier기반의 base learner들을 고려했다고 합니다.

•  예를 들어, K-class lineaer SVM은 \thtea = {w_k}_(k=1~K)로 쓰여질 수 있다고 하는데 음..?
•  Crammer와 Singer는 multi-class SVM을 다음과 같이 형식화 했다고 합니다.

 

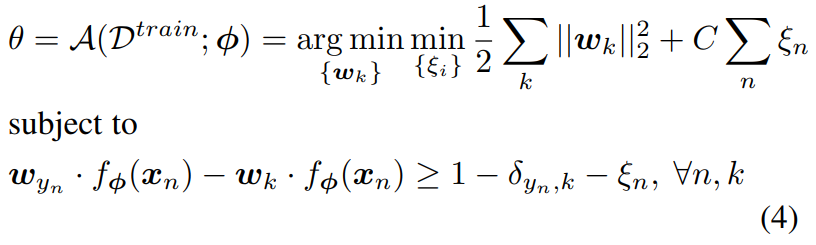
 이때 D^train = {(x_n, y_n)}이라고 하고, C는 regularization parameter이며, \delta는 Kronecker delta function이라고 합니닷

 

 Figure 1에 따르면, 저자들은 자신들의 시스템을 end-to-end train이 가능하게끔 만들기 위해, SVM solver의 solution이 input에 대해 미분 가능하도록 했어야 한다고 합니다. 다시 말해서, 저자들은 밑의 식을 계산할 수 있었어야 한다고 합니다.

•  Objective of SVM은 convex하고 unique optimum을 가지고 있다고 합니다. 이는 necessary gradients를 얻기 위한 KKT condition에 대해 implicit function theorem을 사용할 수 있게끔 해준다고 합니다.

 

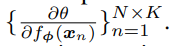
 완비성의 관점에서, 저자들은 convex optimization problem의 이론적인 형태를 유도했다고 하며, 다음의 convex optimization problem을 고려했다고 합니다.

 

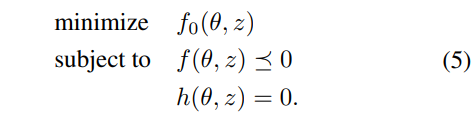
 이때, vector \theta \in R^d는 최적화 변수이며, vector z \in R^e는 input parameter of the optimization problem, which is {f_\phi(x_n)}이라고 합니다.

•  저자들은 다음의 Lagrangian의 안장 점을 찾는 것을 통해, objective를 최적화 할 수 있다고 합니다.

 

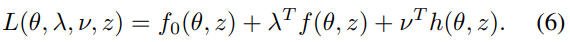
 다르게 말하면, 저자들은 g(\tilde \theta, \tilde \lambda, \tilde v, z)=0을 해결하여 objective function의 optimum을 얻을 수 있다고 합니다.

 

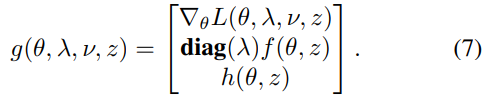
 함수 f(x): R^n → R^m가 주어졌을 때, D_x f(x)는 그 함수에 대한 Jacobian \in R^(m x n)이라고 합니다. 이때, 정리 1은…

⇒ train loss를 최소로 하는 \theta를 closed-form으로 획득 할 수 있게 해주는 식인 것 같습니다.

 

Time complexity.

 저자들이 사용한 접근법인 equation (4)의 계산 즉, forward pass는 num of optimization varibale d에 대해, O(d^3)의 complextiy를 가지는 QP solver의 solution을 필요로 한다고 합니다.

•  이 시간은 KKT matrix primal dual interior point 기법에 필요한 KKT 행렬을 분해 하는 시간에 의해 결정된다고 합니다.

 

 Backwrad pass는 theorem 1에서의 방정식 8의 solution을 요구한다고 합니다. 이 친구는 O(d^2)의 복잡도를 가진다고 하네용.

•  이러한 forward pass와 backward pass는 embedding f_\phi의 차원이 클 때 비용이 비싸질 수 있다고 합니다.

 

Dual formulation

 Equation 4의 objective의 dual formulation은 embedding dimension의 poor dependence를 완화하는 것을 허용해 준다고 합니다. 그리고, 다음과 같이 쓰여질 수 있다고 합니다 후….

 이는 dual variable {alpha^k}_(k=1~K)에 대한 QP의 결과라고함. 저자들은 최적화 변수의 size가 num of training example에 클래스 수를 곱한 값이라고 합니다.

•  이는 few-shot learning의 feature dimension에서의 숫자보다 매우 작은 경우들이 종종 있다고 합니다.
•  저자들은 dual QP 방정식 10을 differentiable GPU-based QP solver를 이용해서 해결했다고 합니다.

 

 실제적으로, table3을 보면 알 수 있다시피, QP solver가 사용한 시간은 ResNet-12 아키텍쳐를 이용해서 feature를 계산하는 시간과 필적하고 그래서 전체적인 iteration별 speed는 Prototypical Network에서 사용된 nearst class prototype과 같은 간단한 base learner기반의 그것들과 많이 다르지 않을 것이라는 얘기를 합니다.

 

 저자들의 work과 동시에, Bertinetto 등은 closed-form solution을 가진 base learner인 ridge regression을 사용했었다고 합니다.

•  비록 ridge regression은 classification problem에 best suite하지는 않지만, 그들의 작업물은 실제 상황에서 one-hot label에 대해 MSE로 훈련시킨 모델이 잘 동작하는 것을 보여주었다고 합니다.
•  Ridge regression의 최적화 결과는 또한 QP이고, 이는 저자들의 framework 내에서 구현될 수 있다고 합니다.

 

Meta-learning objective

 model의 성능을 측정하기 위해, 저자들은 same task로부터 샘플링된 test data의 negative log-likelihood를 평가했다고 합니다.

•  그러므로, 저자들의 meta-learning objective 방정식 2는 다음과 같이 다시 표현할 수 있다고 합니다.

 

 Few-shot learning에서의 이전 연구들은 learnable scale parameter \gamma에 의한 prediction socre를 조정하는 것이 nearest class mean과 ridge regression base learneers아래에서 더 좋은 성능을 제공할 수 있다는 것을 제안했었다고 합니다.

•  저자들 또한 경험적으로 \gamma를 삽입하는 것이 SVM base learner를 사용하는 meta-learning에서도 이점이 있는 것을 확인했다고 합니다.
•  또한 저자들은 hinge loss와 같은 다른 teset loss를 선택하는 것도 가능하지만, log likelihood가 실험에서 가장 좋은 성능을 보였다고 보고했습니다.

 

Experiments

저자들은 먼저, 자신들의 실험에서 사용된 네트워크 구조와 최적화에 관련된 detail들을 4.1에서 설명한다고 합니다.

 

 그 다음, 저자들은 derivatives of Imaganet(4.2) 그리고 CIFAR(4.3)등을 포함하는 표준적인 few-shot classification benchmakrs에서의 결과를 보고한다고 합니다.

•  그 이후에, same embedding network와 training setpup을 사용했을 때, 다양한 base learner를 사용했을 때의 정확도와 속도 면에서의 효과들을 자세히 분석한다고 합니다.

 

Implementation details

Meta-learning setup. 저자들은 관련 연구[18, 20]을 따라, ResNet-12를 자신들의 실험에서 사용했다고 합니다. 자세한 사항은 밑의 사진에서 참고 부탁드려용!

 

 Meta-training 동안, 저자들은 horizontal flip, random crop and color jitter와 같은 [10, 21]에서 사용한 데이터 augmentation 기법들을 사용했다고 합니다.

•  ResNet-12를 이용한 miniImagaNet에서의 실험에서, 저자들은 label smoothing with \epsilon=0.1도 사용했다고 하네요.. 이런 기법도 있었군요?

 

 Meta-testing보다 meta-tarining에 more higher way 분류를 수행한 [28]과 달리, 저자들은 [10, 20]과 같은 최근의 연구를 따라 동일한 stage의 5-way classification을 사용했다고 합니다.

•  각 class들은 meta-training동안 사용할 6개의 test(querey) sample들과 meta-testing 동안 15개의 test sample들을 포함한다고 합니다.
•  저자들의 meta-trained model은 meta-validation set에서의 5-way 5-shot test accuracy를 기반으로 선택된다고 합니다.

 

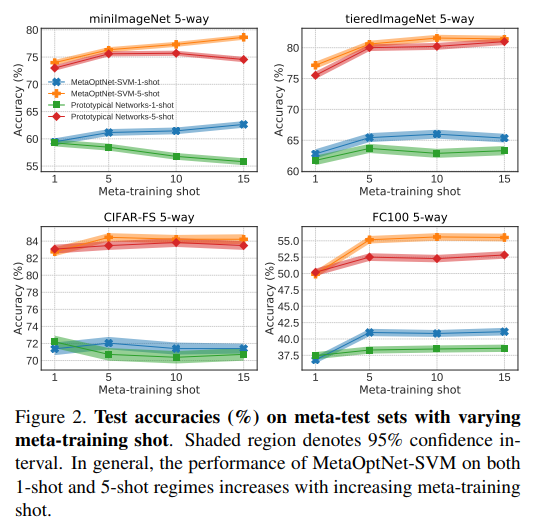
Meta-training shot. Prototypical network에서, 저자들은 meta-training shot과 meta-testing shot과정을 동일하게 가져갔다고 합니다. SVM and ridge regression의 경우, 저자들은 meta-training shot을 meta-test shot 보다 더욱 높게 가져가는 것이 그림 2에서처럼 정확도가 향상된다는 것을 보여주었다고 합니다.

•  그러므로, meta-training동안 저자들은 training shot을 miniImageNet with ResNet에서는 15로, miniImagaNet with 4-layer CNN에서는 5로, tiredImaganet에서는 10으로, CIFAR-FS는 5, FC100은 15로 설정했다고 합니다.

 

Base-learner setup. 선형 분류기 학습의 경우, 저자들은 QP solver인 OptNet을 사용했다고 합니다. SVM에서의 정규화 파라미터 C는 0.1로 했다고 하고, ridge regression에서의 정규화 파라미터 lambda는 50으로 정했따고 합니다.

•  최근접 클래스 평균(prototypical networks)의 경우, 저자들은 metric으로써 Euclidean distance를 사용했다고 합니다.

 

Early stoping. 저자들은 optimizer가 수렴할 때 까지 동작할 수 있음에도 불구하고, 그냥 고정된 수의 iteration동안 solver를 동작 시키는 것이 현실에서 잘 동작한다는 것을 확인했다고 합니다.

•  Early stopping은 추가적인 정규화로써 행동할 수 있고, 꽤나 좋은 성능을 이끌어 냈다고 합니다.

 

Experiments on ImageNet derivatives

 miniImagaNet dataset은 ILSVRC-2012에서 100개의 랜덤 하게 선택된 class로 이루어진 few-shot image classification benchmark라고 합니다.

•  이 클래스들은 64, 16 그리고 20개의 meta-training, meta-validation, meta-testing class들로 나뉜다구 합니다.
• 각 클래스들은 84 x 84 size의 600개의 이미지들로 구성이 되어 있다고 합니다.

 

 tiredImagaNet benchmark는 ILSVRC-2012의 larger subset이라고 하며, 34개의 high-level category 내에서 608개의 class들로 구성되어 있다고 합니다.

•  이는 20개, 6개, 8개의 meta-training, meta-validation, meta-testing을 위한 category들로 나뉜다고 합니다.
•  각각의 category에는 251, 97, 160개의 class가 속해있다고 합니다.

 

Results. Table 1은 5-way miniImageNet and tieredImagaNet의 결과를 요약해서 보여주고 있다고 합니다.

•  저자들의 기법은 해당 benchmark에서 5-way SOTA성능을 달성했다고 합니다.

 

 LEO는 encoder와 relation network를 WRN-28-10에 추가하여 gradient descent에 대한 초기화를 잘 했다고 합니다. MAML 비슷한 느낌인거일려나요?

 TADAM은 task embedding network(TEN) block을 각 convolutional layer에 적용하여 element-wise scale and shift vectors를 예측했다고 합니다.

 

 이전 연구들은 feature extraction을 위한 부분과 base learner를 따로따로 가지고 있으며, few-shot시 앞 단을 freeze하는 방법을 사용한다는 점을 지적

•  저자들의 기법은 대조적이게도, end-to-end로 meta-train된다고 하며, 이러한 전략이 meta-learning에서 효과적이었다는 것을 실험으로 확인했다는 식으로 서술함.

 

Experiments on CIFAR derivatives

 CIFAR-FS dataset은 최근에 제안된, CIFAR-100의 모든 100개의 class들로 이루어진 few-shot image classification benchmark라고 합니다.

•  해당 class들은 64, 16, 20개의 meta-training, meta-validation, meta-testing을 위한 class로 randomly split되며, 각 클래스는 32 x 32의 600개의 image들로 구성되어 있다고 합니다.

 

 FC100 dataset은 CIFAR-100으로부터 유도된 다른 데이터셋이며, 20개의 super class로 그루핑 된 100개의 클래스들을 포함하고 있다고 합니다.

•  이 클래스들은 각각 60 classes from 12 superclasses, 20 classes from 4 super classes, 20 classes from 4 superclasses로 meta-training, meta-validation, meta-testing을 위해서 나뉜다고 합니다.
•  각 클래스는 위와 동일하게, 32 x 32의 600개의 image들로 구성되어 있다고 합니다.

 

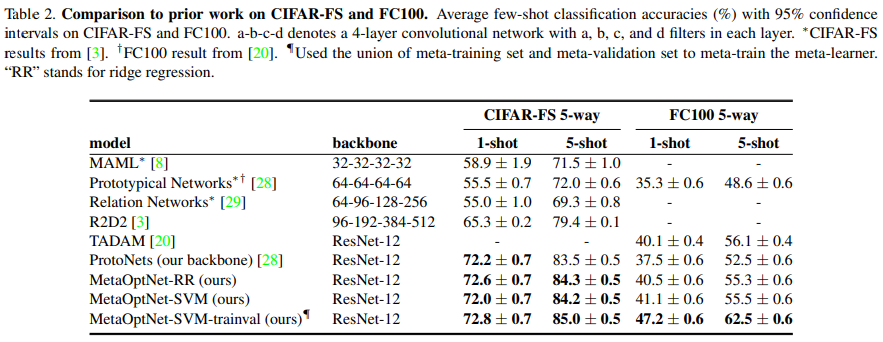
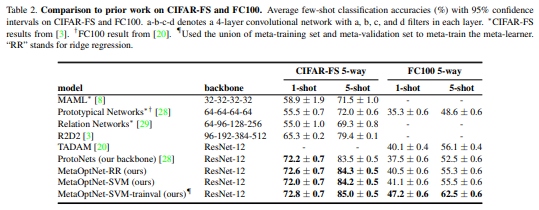
Results. Table2는 5-way classification tasks에 대한 결과를 요약해서 보여주고 있으며, 저자들의 MetaOptNet-SVM이 SOTA 성능을 달성했다고 합니다.

•  더 어려운 FC100에 대해서, 이 차이는 더욱 상당했다고 합니다. 이는 complex base learner를 few-shot learning setting에서 사용했을 때의 이점을 강조한다고 합니다.

 

Comparisons between base learners

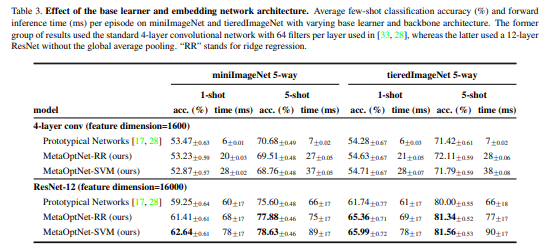
 Table3는 two different embedding architecture에 대해, base learner를 변화시켜가며 얻은 결과라고 합니다.

•  저자들은 4-layer convolutional network(1600 feature dimension)을 사용했을 때, few-shot learning을 위한 discriminative classifier를 채택해도 큰 이득이 없었다고 얘기합니다.
•  실제로, 최근접 이웃 기반 classifier는 low-dimensional feature 하에서도 동작이 잘 됬다고 얘기합니다. (Prototypical network 처럼)

 

 그러나, embedding dimension이 16000 정도로 굉장히 높은 경우에, SVMs은 다른 base learner들에 비하여 더 좋은 few-shot accuracy를 보였다고 하고 있습니다.

•  Thus, 정규화된 선형 분류기들도 높은 차원의 feature가 이용 가능하면, 어느 정도 강건한 성능을 보였다고 하네요.

 

 이러한 benefit의 증가는 computational cost의 증가를 가져왔다고 합니다. ResNet-12의 경우, 최근접 분류기에 비교하여 13%정도 추가적인 overhead가 ridge regression base learner에서 발생 했고, 30~50% 정도 추가적인 overhead가 SVM base learner에서 발생했다고 합니다.

 

 Figure2를 보면, 1-shot, 5-shot 영역에서의 저자들의 모델의 성능은 meta-training shot이 증가할수록 증가하는 것을 볼 수 있다고 합니다.

•  이는 모든 meta-test shot에 대해 더 많은 shot을 meta-training에서 활용할 수 있으므로, 저자들의 기법을 더욱 실용적인 접근으로 만들어준다고 합니다.

 

 FC 100 실험에서 보고 된 것처럼, SVM base learner는 test와 train에 쓰인 data간의 semantic overlap이 더 적을 때, 이점을 가지는 것으로 보인다고 서술함.

 

 저자들은 class embedding들이 test data보다 train data에 대해 훨씬 더 compact하다고 가정한다고 합니다. 따라서, base learner의 flexibility는 noisy embedding에 대한 강건성을 가지게 해주고, 일반화 성능을 높여준다고 서술했습니다.

 

Reducing meta-overfitting

Augmenting meta-training set. Task들을 sampling하는 것에도 불구하고, MetaOptNet-SVM with ResNet-12의 meta-training의 종료 시점에는 tiredImageNet을 제외하고, 모든 meta-training dataset들에 대해서 거의 100%의 test accuracy를 보였다고 합니다.

•  해당 overfitting을 완화시키기 위해, [21, 25]와 유사하게, 저자들은 meta-training과 meta-validation set의 합집합을 사용해, epoch와 같은 hyperparameter등은 이전 셋팅과 동일하게 유지하면서 임베딩을 meta-training했다고 합니다.
•  특히, 저자들은 miniImageNet에서는 21 epoch이후에, tieredImageNet에서는 52 epch 이후에, CIFAR-FS와 FC 100에서도 각각 21 epoch이후에 meta-training을 종료했다고 합니다.
•  Table 1과 2는 augmented meta-training set의 결과를 보여주고, 이 결과를 MetaOptNet-SVM-trainval으로 명명해두었다고 합니다.

 

 miniImageNet, CIFAR-FS 그리고 FC100 dataset들에서, 저자들은 test accuracy의 개선을 관측했다고 합니다. 그런데 아쉽게도, tiredImageNet dataset에서의 차이는 미미했다고 하네요.

•  저자들은 이것이 그들의 시스템이 overfitting의 영역에 들어가지 못 해서 그런 것이라고 해석했습니다. (사실, tiredImagaNet meta-training에서 94%까지의 정확도는 보았다고 하네요.)

 

 저자들의 결과는 더 많은 meta-training class들이 meta-learning embedding의 meta-training set에 대한 overfitting을 줄이는 것을 도와줄 수 있는 것을 보여준다고 합니다.

 

Various regularization techniques. Table 4는 ResNet-12로 이뤄진 MetaOptNet-SVM에서의 정규화 기법들에 대한 효과를 보여준다고 합니다.

•  저자들은 few-shot learning에서의 초기 연구인 [28, 8]이 이러한 기법들을 적용하지 않았음을 알린다고 합니다.
•  저자들은 regularization을 사용하지 않았을 때, ResNet-12의 성능은 조그마한 CNN정도의 성능으로 줄어든다고 하며, 이를 Table 3에서 보여주었다고 합니다.

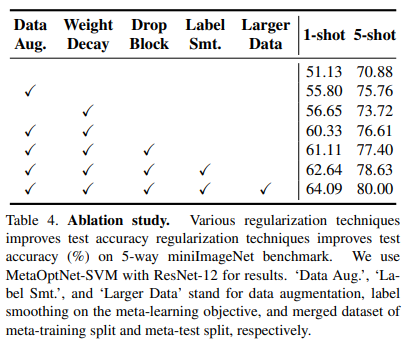
 이는 meta-learner들을 위한 정규화의 중요성을 보여준다고 합니다. 저자들은 few-shot learning system들의 성능이 새로운 정규화 기법들을 도입함에 따라 더욱 향상될 수 있으리라 기대한다고 합니다.

 

Efficiency of dual optimization

 Dual optimization이 실제로 효과적이고 효율적인지 확인하기 위해, 저자들은 QP solver의 iteration을 변화해가며 meta-test의 정확도를 측정했다고 합니다.

•  QP solover의 각 iteration은 KKT matrix의 LU decomposition을 통해 primal과 dual update를 계산하는 과정을 포함한다고 합니다.
•  결과는 Figure3에 도시되어 있다고 합니다.

 

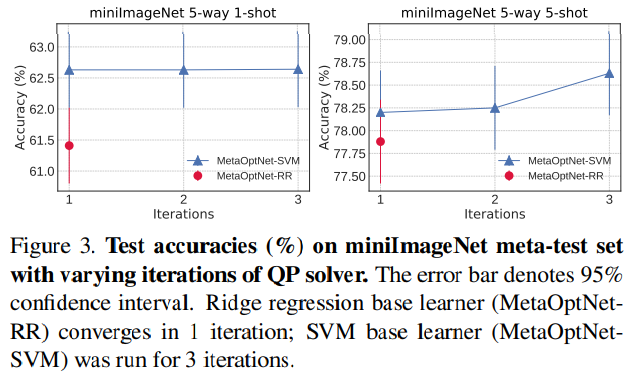
 QP solver는 just one iteration안에 ridgi regression objective의 최적점에 도달했다고 합니다.

• 대안적으로, [3]에서 사용한 closed-form solution을 사용할 수도 있다고 합니다.

 

 또한, 저자들은 1-shot task들에 대해서, QP SVM solver가 비록 KKT condition이 정확히 만족 되지 않음을 관찰했지만, 1 iteration만에 optimal 정확도에 도달할 수 있었다고 합니다.

 

 5-shot task들에 대해서는, 심지어 QP SVM solver를 1 iteration만 돌렸음에도, other base learner들에비해 더 좋은 정확도를 달성할 수 있었다고 합니다.

 

 또한, 저자들은 SVM solver의 iteration이 1 iteration으로 제한 되었을 때, ridge regression solver와 계산 비용이 비슷했다는 것을 Table3에서 구체적인 수치로 보여주었다고 합니다.

 

 이러한 실험들은 SVM과 ridge regression의 dual objective를 푸는 것이 fet-shot setting 아래에서 매우 효율적임을 보여준다고 합니다.

 

Conclusions

 해당 논문에서, 저자들은 few-shot learning을 위해 convex base learner를 이용하는 meta-learning approach를 보여주었다고 합니다.

 

 Dual formulation과 KKT condition은 few-shot learning problem에 특히 적합한 meta-learning에서의 계산 효율과 메모리 효율을 허용하기 위해 십분 이용이 되었다고 합니다.

 

 Linear classifier는 약간의 computational cost의 증가 만으로, 최근접 이웃 분류기보다 더욱 좋은 일반화 성능을 제공했다고 합니다.

 

 저자들의 실험들은 정규화된 선형 모델들이 overfitting을 줄이면서도 상당히 높은 embedding dimension을 허용한다는 것을 보여주었다고 합니다.

 

 Future work으로는, 저자들은 kernel SVM들과 같은, 다른 convex base-learner에 대해서 해당 기법을 적용해보는 것을 목표로 하고 있다고 합니다.

•  저자들은 이를 통해 task에 더 많은 훈련 데이터를 사용할 수 있게 되고, 모델의 capacity를 점진적으로 늘릴 수 있을 것이라고 얘기합니다.